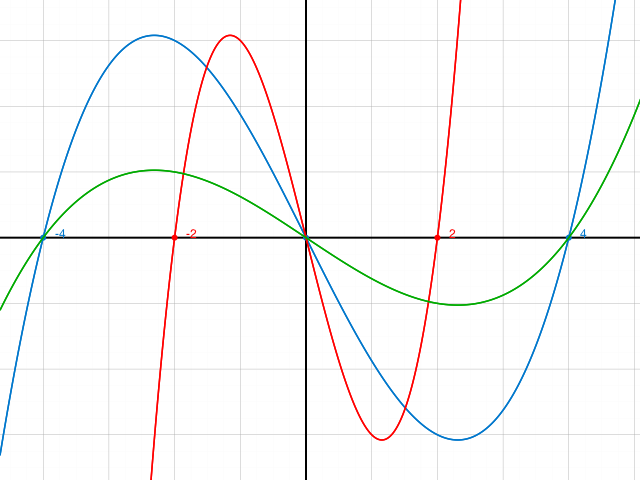
Die Abb. D.1 zeigt den Graph f1 von f(x) = x^3 -4x für 0 > sowie den entlang der x-Achse gedehnten Graph f2 und den entlang der x- und y-Achse gedehnten Graph f3. Bestimmen Sie die Funktionsgleichung der Graphen.
Damit die Nullstellen dort sind, wo sie sind, müssen die entsprechenden Linearfaktoren vorkommen.
f1(x) = x^3 -4x = x(x^2 - 4) = x (x-2)(x+2). NS: 0 , 2 , - 2: rote Kurve
NS von f2 und f3 : 0, 4, -4
Streckung in x-Richtung (Faktor 2) : x-Werte halbieren: blaue Kurve
f2(x) = (x/2)((x/2) - 2)((x/2) + 2)
Streckung in y-Richtung: y-Werte ( also Funktionswerte) durch 3 dividieren.
f3(x) = (1/3) (x/2)((x/2) - 2)((x/2) + 2) : grüne Kurve