a) Von einem Rechenviereck ist bekannt, dass die Randzahlen \( a+b=20, a+c=5, b+d=25 \) und \( c+d=10 \) sind. Ermitteln Sie alle Möglichkeiten für die Innenzahlen \( a, b, c \) und \( d \).
b) Wir betrachten nun den allgemeinen Fall: Von einem Rechenviereck sind nur die Randzahlen \( w, x, y \) und \( z \) bekannt (diese Zahlen müssen nicht notwendigerweise voneinander verschieden sein).
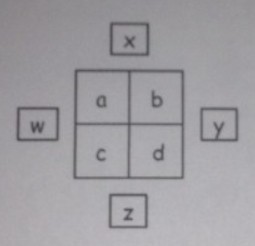
Stellen Sie das zugehōrige lineare Gleichungssystem auf und ermitteln Sie, in welchem Fall es keine Lösung, genau eine Lösung bzw. unendlich viele Lösungen gibt. Geben Sie jeweils die Lōsungsmenge explizit an.