Wie soll ich hier die Nullstellen berechnen: fa(x) = x3 - 3a2*x + 2a3

Question

Hallo

Kann mir jemand erklärne, wie man hier die NST berechnet ?

fa(x) = (x)³-3(a)²*x+2(a)³

Answer 1

Du musst eine Nullstelle raten. Da geht das beispielsweise mit

x = -2,

damit eine Polynomdivision machen

(x³-3a²*x+2a³) : (x+2a) = x²-2ax+a²

Für letzteres erkennt an die binomische Formel:

x²-2ax+a² = (x-a)²

Also:

x_1,2 = a

x₃ = -2a

Grüße

Answer 2

"

die NST berechnet ?

fa(x) = (x)³-3(a)²*x+2(a)³

einfach genau hinschauen:

welcher besondere Wert für x " passt"  denn da genau ?

.

Answer 3

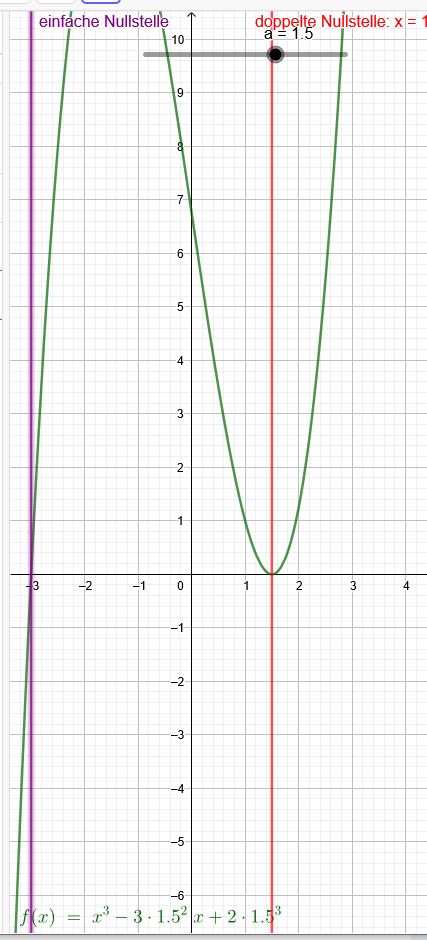
$f(x)=x^3-3a^2x+2a^3$

$f'(x)=3x^2-3a^2$

$3x^2-3a^2=0$

$x_1=a$   → $f(a)=a^3-3a^2\cdot a+2a^3=0$

An der Stelle $x=a$   ist somit eine doppelte Nullstelle (Extremum)

Polynomdivision:

$(x^3-3a^2x+2a^3):(x-a)^2=(x^3-3a^2x+2a^3):(x^2-2ax+a^2)$

  $(x^3-3a^2x+2a^3):(x^2-2ax+a^2)=x+2a$

$-(x^3-2ax^2+a^2x)$

.................................

           $2ax^2 -4a^2x +2a^3$

        $-(2ax^2-4a^2x+2a^3)$

-----------------------------------------

                    $0$

Eine einfache Nullstelle liegt nun bei $x=-2a$