Im R4 seien folgende Tupel eines Unterraumes gegeben. Bestimme die Dimension und je eine Basis des Unterraumes

Question

 

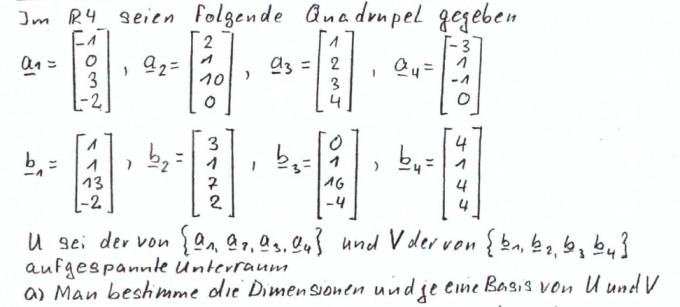
ich habe eine Problem mit folgender Aufgabe. Mein Problem besteht darin eine Basis für den Unterraum U aufzuschreiben.

Mein bisheriger Lösungsansatz:
um die Dimension zu ermitteln muss ich die Anzahl der linear unabhängigen Vektoren herausfinden, da diese den Unterraum aufspannen. Dies mache ich in dem ich die Quadrupel Zeilenweise aufschreibe und umforme.

$$\begin{matrix} { a }_{ 1 } & = \\ { a }_{ 2 } & = \\ { a }_{ 3 } & = \\ { a }_{ 4 } & = \end{matrix}\begin{pmatrix} -1 & 0 & 3 & -2 \\ 2 & 1 & 10 & 0 \\ 1 & 2 & 3 & 4 \\ -3 & 1 & -1 & 0 \end{pmatrix}\overset { durch }{ \underset { Umformung }{ \longrightarrow } } \begin{pmatrix} -1 & 0 & 3 & -2 \\ 0 & 1 & 16 & -4 \\ 0 & 0 & -26 & 10 \\ 0 & 0 & 0 & 0 \end{pmatrix}$$

Könnte ich das ganze auch in Komponenten Schreibweise gestalten, sprich ich reihe die Quadrupel nebeneinander zu einer 4x4 MAtrix und forme dann um ?

Demnach habe ich 3 linear unabhängige Vektoren und mein Unterraum hat die Dimension 3.

Und nun zu meinem Problem. Wie sieht eine beliebige Basis des Unterraums aus? Hat sie 3 oder 4 Vektorkomponenten

$$\begin{pmatrix} { e }_{ 1 } \\ { e }_{ 2 } \\ { e }_{ 3 } \end{pmatrix}\quad oder\quad \begin{pmatrix} { e }_{ 1 } \\ { e }_{ 2 } \\ { e }_{ 3 } \\ { e }_{ 4 } \end{pmatrix}$$

Kann ich 3 willkürliche Vektoren nehmen die nicht linear von einander abhängig sind z.B.

$${ basisvektor }_{ 1 }\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},{ basisvektor }_{ 2 }\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},{ basisvektor }_{ 3 }\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}\quad (bzw.\quad mit\quad 4\quad Vektorkomponenten)$$

Ich hoffe es kann mir jemand weiter helfen,

Answer 1

Es geht doch um die Basis des Untervektorraumes. Damit musst du auch 4 Dimensionale Vektoren haben. Du kannst direkt deine Zeilen nehmen.

[-1, 0, 3, -2]; [0, 1, 16, -4]; [0, 0, -26, 10]

Comments

Okay vielen dank das hilft mir sehr.

Eine Frage hätte ich noch, Interesse halber. Könnte ich auch andere Basis Vektoren nehmen, wenn ja welche Eigenschaften müssten diese aufweisen?

---

Sie sollten eine Basis bilden. Dafür hast du ja das Gauss-Verfahren angewendet.