Funktionsgleichung aufstellen anhand von zwei Tiefpunkten.

Question

Ich komme nicht mit der 4b ganz klar,Wie kann ich denn anhand so wenig Information die Funktionsgleichung aufstellen?

Comments

Wie kann ich denn jetzt auch noch herausfinden welchen Grad die Funktion hat?

---

f'(0) = 0

f(0) = 0

f(2) = -4

f'(2) = 0

Die Funktion ist achsensymmetrisch zu y-Achse.
Die Funktion darf nur Terme mit geradem Exponenten haben.

Probieren wir einmal

f ( x ) = a*x^4 + b*x^2 + c
f ( 0 ) = a*0^2 + b*0^2 + c = 0  => c = 0

f ( x ) = a*x^4 + b*x^2
f ´ ( x ) = 4 * a * x^3 + 2 * b * x
f ´( 0 ) = 0 | keine neuen Informationen

Es bleibt
f(2) = -4
f'(2) = 0

f ( x ) = a*x^4 + b*x^2
f ( 2 ) = a * 2^4 + b*2^2 = 16a + 4b = -4
f ´ ( x ) = 4 * a * x^3 + 2 * b * x
f ´ ( 2 ) = 4 * a * 2^3 + 2 * b * 2 = 32a + 4b = 0

16a + 4b = -4  | * 2
32a + 4b = 0

32a + 8b = -8 
32a + 4b = 0
-----------------
8b - 4b = -8
4b = -8
b = -2

32a + 4b = 0
32a + 4*(-2) = 0
32a -8 = 0
a = 1/4

Answer 1

f'(0) = 0

f'''(0) = 0

f(0) = 0

f(2) = -4

f'(2) = 0

Helfen tut dann: http://www.arndt-bruenner.de/mathe/scripts/steckbrief.htm

f(x) = 0,25·x^4 - 2·x^2

Comments

Die Funktion hat ja 4 Extremstellen.Warum ist die Funktion jetzt 4.Grades und nicht 5.?

---

Wo siehst du bitte 4 Extremstellen ?

---

ach ich meine 2..die zwei Tiefpunkte halt auf dem Graphen.Der Graph ist deswegen achsensymmetrisch?

---

ich hab für c=0 ist das richtig?

---

Ich bitte dich. wir haben 3 Extrempunkt.

TP(-2|-4) ; HP(0|0) ; TP(2|-4)

Also bis 3 zu zählen sollte noch drin liegen.

Wenn man 3 Extrempunkte hat braucht man mind eine Funktion 4. Grades.

---

ich hab für c=0 ist das richtig?

Ich habe oben bereits die Lösung hingeschrieben, damit du nicht nachfragen brauchst wenn du etwas heraus hast. Du brauchst nur nachfragen, wenn du etwas anderes heraus hast. Entweder hab ich dann ein Fehler gemacht oder du.

---

16a+4b=-4..Nach diesem Teil komm ich nicht mehr weiter.Wie kann ich das denn auflösen und danach a und b ermitteln?

---

wenn ich das halt durch 16 teile kommt diese -0,25 raus.Wo liegt denn mein Fehler?

---

Du solltest 2 Gleichungen mit 2 Unnekannten haben sonst kannst du es nicht lösen.

---

32a+4b=-4

16a+4b=0

Diese Funktion habe ich subtrahiert dann kam am ende 16a=4..Habe danach durch 4 geteilt dann kam für a=0,25

Ist dieser Rechenweg akzeptabel?

---

32a+4b=-4

16a+4b=0

I - II

16a = -4 --> a = -1/4

Du musst daher wohl einen Fehler haben denn hier würden laut lösung +1/4 heraus kommen.

---

Wo steckt denn der Fehler ?Ich hab die 1.Gleichung minus die 2.Gleichung gemacht.Könntest du mir den richtigen Rechenweg für die Ermittlung von a mal zeigen bitte?

---

f(x) = ax^4 + bx^2 + c

f(0) = 0 --> c = 0

f(2) = -4 --> 16·a + 4·b = -4

f'(2) = 0 --> 32·a + 4·b = 0

II - I

16a = 4 --> a = 1/4

32·(1/4) + 4·b = 0 --> b = -2

---

Danke dir hab bei 32a+4b=-4  einen fehler gemacht das müsste =0 lauten.Trotzdem vielen dank nochmal

Answer 2

Du sollst eine  mögliche Funktionsgleichung bestimmen:

Der Graph passt zu f(x) = ax⁴ +.....

f(x) = ax⁴ + bx² + c [Symmetrie zur y-Achse]

f(0) = 0

f(2) = -4

f ' (2) = 0

ergibt das GLS

Comments

Woher weisst du denn dass der Graph zu 4.Grades passt?Wie findet man das raus

Answer 3

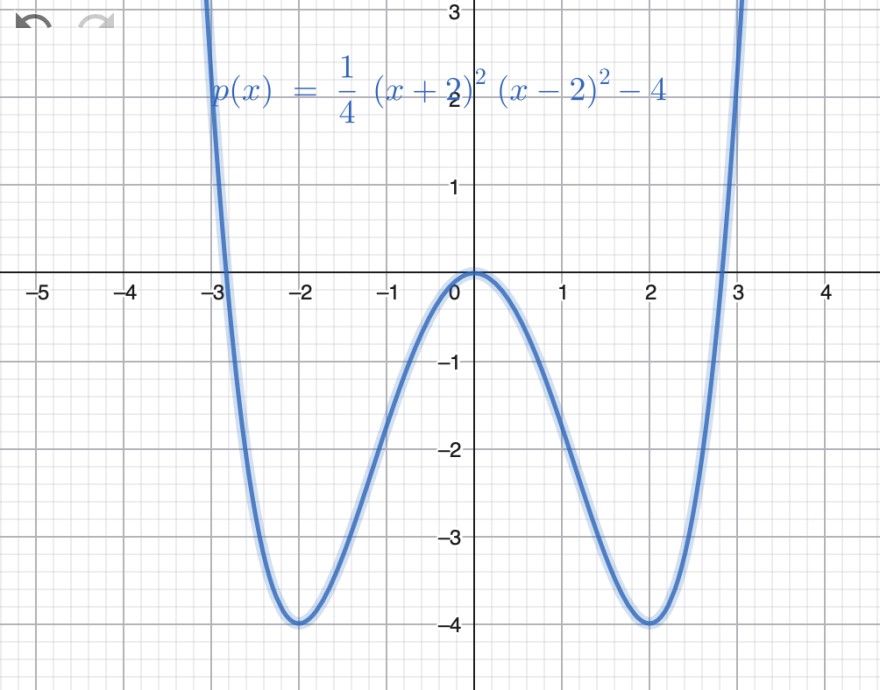
4b) 

Der Graph ist achsensymmetrisch.   Da 3 Extrempunkte vorliegen, handelte sich um Grad 4

\( T_1(-2|-4)\)und \( T_2(2|-4)\)

Ich verschiebe den Graphen um 4 Einheiten nach oben, weil dann die Tiefpunkte auf der x-Achse liegen:  \( T´_1(-2|0)\)und \( T´_2(2|0)\)

\(f(x)=a(x+2)^2(x-2)^2 \)

Der Hochpunkt hat die Koordinaten \( H(0|0)\)  → \(  H´(0|4)\)

\(f(0)=a(0+2)^2(0-2)^2 =16a=4\)

\(a=\frac{1}{4}\)

\(f(x)=\frac{1}{4}(x+2)^2(x-2)^2 \)

Nun noch um 4 Einheiten nach unten verschieben:

\(p(x)=\frac{1}{4}(x+2)^2(x-2)^2-4 \)