normale Winkelberechnung 7. Nr 45

Question

Die Lösung ist 27 Grad. Ich komme aber immer auf 21 oder 30 Grad, weil ich in der Mitte ein gleichseitiges Dreieck nehme.. Wäre dankbar, wenn ihr mir helfen könnte.

Comments

Vom Duplikat:

Titel: Eigenmann: Nummer 45, Teil 1

Stichworte: geometrie,eigenmann,eigenmann-1-1,gleichschenkliges-dreieck

Aufgabe:

Wie groß ist der Winkel α?

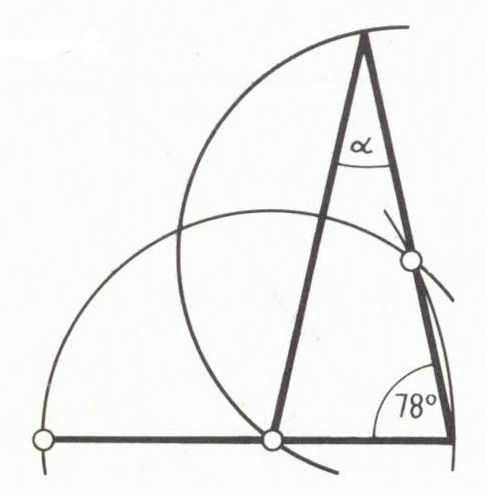
Ohne Taschenrechner; die Figuren sind nicht maßgetreu.

Paul Eigenmann, Aufgabe 1.1.45, ISBN 3-12-722310-2, 1981, S. 9

Problem/Ansatz:

Nebenbemerkung:
Die Skizze ist merkwürdig: Wo ist anzufangen, und wie geht es weiter, wenn man sie für eine zeichnerische Lösung nachzeichnen wollte?

---

... wenn man sie für eine zeichnerische Lösung nachzeichnen wollte?

waagerechte Linie

unterer Halbkreis

Gerade vom Punkt unten links im Winkel 180 Grad minus 2 mal 78 Grad

rechte Seite des Dreiecks und Halbkreis der durch die obere Dreiecksecke geht

linke Seite des Dreiecks

---

döschwo

waagerechte Linie

unterer Halbkreis

Gerade vom Punkt unten links im Winkel 180 Grad minus 2 mal 78 Grad

rechte Seite des Dreiecks und Halbkreis der durch die obere Dreiecksecke geht

linke Seite des Dreiecks

Danke für diese Zeilen. Das gleichschenklige Dreieck mit den Basiswinkeln 24° ist der Clou.
Wie vermutet, es ist unklar, wie die Aufgabe gemeint ist. Der zweite Punkt auf der Grundlinie muss erst konstruiert werden, damit der Winkel α zu seinem linken Schenkel kommt.

---

Gerade vom Punkt unten links im Winkel 180 Grad minus 2 mal 78 Grad

setzt eine algebraische Rechnung ein, wie man sie für eine zeichnerische Lösung vermeiden kann :

1. Winkel von 78° mit dem Scheitelpunkt S und den Schenkeln a und b.
2. Punkt A auf a beliebig
3. Mittelsenkrechte m von A und S schneidet b in B.
4. Mittelsenkrechte n von A und B schneidet b in C.
5. Kreis um A durch C schneidet a in D.
6. α = ∠CDS

---

Eigenmann hat auch Lösungen mitgeliefert. Zu dieser Aufgabe schrieb er:

[spoiler]

\(\displaystyle 27^\circ \)

[/spoiler]

(eingangs zitiertes Werk, S. 57)

Tschät-tschi-pi-ti nennt 39 Grad ...

---

gasthj2166

algebraische Rechnung, [die man] für eine zeichnerische Lösung vermeiden kann.

Gut; es geht auch so, den Punkt C zu finden,

Meine Meinung, dass uns Eigenmann systematisch etwas im Dunklen lässt, wird davon nicht berührt. Was ist Deine Meinung zu meinem Empfinden?

---

Die in der Aufgabe dargestellte Situation war nie dazu gedacht konstruiert zu werden, sondern es ging Eigenmann um eine Rechnung wie du sie ausgeführt hast.

---

.                                           gelöscht

---

dass uns Eigenmann systematisch etwas im Dunklen lässt ...

Eigenmann ging vielleicht von der Annahme aus, "helle Köpfe bringen Licht ins Dunkel."

Der Herr Pascal (der mit dem Dreieck, und dem Luftdruck, und der Programmiersprache) sagte es so: "Qu'il regarde cette éclatante lumière mise comme une lampe éternelle pour éclairer l'univers ..." Mit weniger als der Ewigkeit und dem Universum gab er sich nicht zufrieden. Dem Eigenmann genügten schon Dreiecke.

Answer 1

vom Mittelpunkt unten nach links bzw. nach schräg rechts hast Du den Radius r, ebenso vom rechten Punkt nach unten Mitte und nach oben. D.h. die beiden Kreise sind gleich groß und die Figur ist symmterisch zur Winkelhalbierenden von 78. Verbindest Du den linken mit dem rechten Mittelpunkt ist das untere Dreieck gleichschenklig, das andere somit auch.

Grüße,

M.B.

Answer 2

Hier meine Skizze:

Ich komme damit auf einen Winkel von 1.5·78 - 90 = 27 Grad.