Koordinatensystem drehen

Question

Ein(x,y,z) Koordinatensystem wird in drei aufeinanderfolgenden Schritten gedreht.
1) Drehungum die z-Achse in math. pos. Sinn um 30°
2) Drehung um die neue y-Achse in math. pos. Sinn um 45°
3) Drehung um die neue x-Achse in math. pos. Sinne um 60°
Das so entstandene neue System sei mit (xn,yn, zn) bezeichnet.
Welche Drehmatrix D führt die alten Ortsvektoren x über in die neuen Ortsvektoren xn mit xn=D*x ?
Welche Koordinaten hat der Punkt P (3 /-2/5) im neuen Koordinatensystem?
Welchen Winkel schließt die neue yn-Achse mit der alten z-Achse ein?

Kann mir jemand helfen, Ansätze oder wie das gehen soll?

Answer 1

Hallo Rike,

Dreht man ein Koordinatensystem um die Z-Achse um den Winkel $\Theta$, so kann man das neu entstandene Koordinatensystem (1-System) bezogen auf das vorherige (0-Sytem) wie folgt beschreiben: $$^0T_1=\begin{pmatrix} \cos \Theta & -\sin\Theta & 0 \\ \sin\Theta & \cos\Theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$$ die erste Spalte dieser Matrix beschreibt die Lage der neuen X-Achse $^1\vec{n}$ im alten System. Ich nenne sie hier $\vec{n}$ für Normalrichtung.

damit kann man jetzt Koordinaten, die im neuen System (1-System) angegeben sind, in das alte (0-System) in das umrechnen. Allgemein gilt $$^0\vec{x}=^0T_1\cdot ^1\vec{x}$$ Da wir später aber die Transformation von alt nach neu benötigen, berechnen wir die Inverse. In diesem Sonderfall ist die Inverse gleich der Transponierten. Es gilt $$^1T_0={(^0T_1)}^{-1}={^0T_1}^{T}=\begin{pmatrix} \cos \Theta & \sin\Theta & 0 \\ -\sin\Theta & \cos\Theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$$ Ich habe die drei Systeme mit 1, 2 und 3 benannt. Das dritte  ist das n-System aus Deiner Aufgabe. Anbei die konkreten Werte:

 

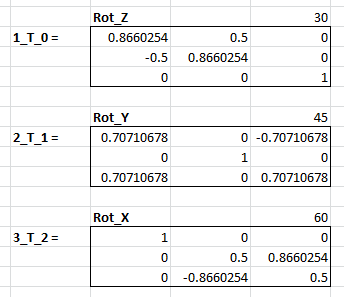
Die gesuchte Drehmatrix D ist nun identisch mit $^3T_0$. Es gilt $$D=^3T_0=^3T_2\cdot^2T_1\cdot^1T_0$$

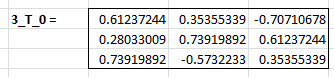
Ein Punkt $^0P$ im alten Sytem (0-System) lässt sich nun in das neue (3-System) umrechnen $$^3P=^3T_0\cdot ^0P= ^3T_0\cdot\begin{pmatrix} 3 \\ -2 \\ 5 \end{pmatrix} \approx \begin{pmatrix} -2,406 \\ 2,424 \\ 5,132 \end{pmatrix}$$

Den Winkel zwischen neuer Y-Achse und alter Z-Achse bekommt man aus dem Skalarprodukt der beiden Achsen. Es ist dabei egal in welchem System man rechnet! Da ich beide Achsen nur im 3'er-System zur Verfügung habe - nehme ich dies her. Ich nenne die Y-Achse $\vec{o}$ und die Z-Achse $\vec{a}$. Aus der Matrix oben lässt sich herauslesen $$\vec{o}_3 \cdot ^3\vec{a}_0=\begin{pmatrix} 0\\ 1\\ 0\end{pmatrix} \cdot \begin{pmatrix} -0,707\\ 0,612\\ 0,354\end{pmatrix}=0,612$$ D.h. der Winkel beträgt etwa 52,2°.

Zur Schreibweise mit den führenden Indizes siehe auch hier: Denavit-Hartenberg

Gruß Werner

Comments

Dankeschön und ich habs sogar verstanden! Gruß Rike

Answer 2

1) Drehung um die z-Achse in math. pos. Sinn um 30°

Dabei bleibt ja die z-Koordinate unverändert   und aus

1                           cos(30°)                      (√3) / 2
0            wird        sin(30°)              =           1 / 2
0                                0                                   0

und aus

0                         - sin(30°)                             -1/2
1          wird           cos(30°)            =           (√3) / 2
0                                0                                      0

und aus

0                             0
0           wird           0
1                             0

Und die Spalten der gesuchten Matrix sind ja immer die
Bilder der kanonischen Basisvektoren, also ist die Matrix
für die erste Drehung:

(√3) / 2       -1/2          0
  1/2          (√3) / 2      0
   0                0           1

So ähnlich bekommst du die anderen Drehmatrizen auch
hin und bildest dann das Produkt der drei ( in der richtigen
Reihenfolge, also mit der letzten beginnen.)