Grenzwert einer unendlichen Summe

Question

 Ich versuche mich nun schon ewig an dieser ( bzw. Aufgaben ähnlichen Typs) und habe bislang sowohl hier als auch im Internet und in Lehrbüchern nie die Lösung/den Ansatz zu genau dieser Aufgabe gefunden...
"Berechnen Sie im Falle der Existenz folgende Grenzwerte, beziehungsweise zeigen Sie andernfalls, dass die Grenzwerte nicht existieren." 

$$\sum _{ n=3 }^{ \infty }{ \frac { 2·{ 4 }^{ n } }{ { 6 }^{ n-2 } } }$$ 
Oft wurde hier die Partialbruchzerlegung genannt, aber ich bin bis jetzt auch nicht darauf gekommen wie ich diese nun auf meine Aufgabe anwenden kann...:/ 
Ich wäre euch für einen Ansatz /eine grobe Anleitung sehr Dankbar!!

Answer 1

mssxx,

wir beginnen mit einem kleinen Rechentrick. Es ist $$\dfrac{6^2}{6^2}=1$$ Diesen Wert multiplizieren wir mit der gegebenen Reihe, was wir dürfen, da wir im Prinzip nur mit 1 multiplizieren). Jetzt können wir mit den Potenzgesetzen Folgendes tun: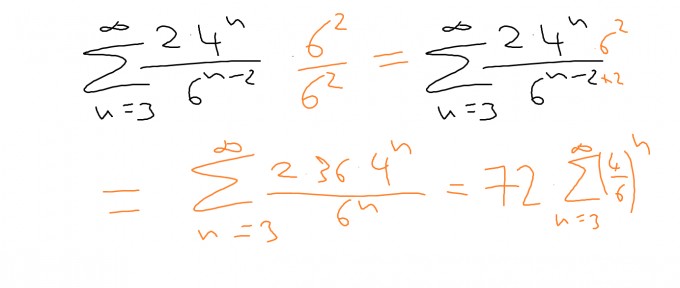 

Es liegt nun eine geometrische Reihe mit $$|p|<1$$

vor, die wir von n=3 bis unendlich berechnen. Die Grenzwertformel für die geometrische Reihe lautet:

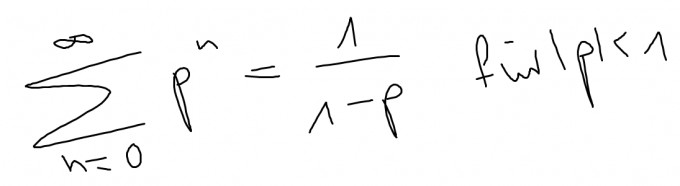
Diese Formel beginnt jedoch bei n=0. Es gilt mit unseren Werten: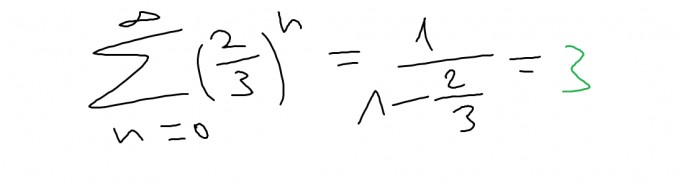 

Von diesem Wert subtrahieren wir noch folgende Elemente (die obige Formel beginnt bei n=0, in der Aufgabe wird bei n=3 gestartet, d.h. n=0, n=1 und n=2 wird abgezogen): 

Dieses Ergebnis wird zum Schluss mit 72 multipliziert, da wir das als Faktor vor die Summe gezogen haben. Das Ergebnis lautet also: $$72\cdot \dfrac{8}{9}=64$$ Ein Beweis, dass diese Rechnung zu einem sinnvollen Ergebnis führt, findest Du hier: https://www.wolframalpha.com/input/?i=sum+n%3D3+to+infinity++(2*4%5E…

Konnte ich Dir weiterhelfen? Bei Rückfragen kannst Du Dich gerne wieder melden.

André, savest8

Comments

Vieeelen herzlichen Dank!!

Der erste Teil hat mir einfach gefehlt! Nur eine kurze Nachfrage: Lässt sich dieses Vorgehen grundsätzlich auch auf andere Aufgaben diesen Typs übertragen, oder ging dieser "Trick" nur in dem Fall?:)

---

Gerne doch! Ich freue mich, dass Du die Aufgabe verstanden hast:-)
Im Prinzip kannst Du dieses Vorgehen zur Umformung immer verwenden, denn Du machst schließlich nichts anderes als mit 1 zu multiplizieren. Du musst lediglich den Exponenten der Zahl für diesen Trick entsprechend dem Wert des Minuenden (bei n-2 also die 2) anpassen. 


André, savest8

---

Ich habe mich jetzt mal spaßeshalber an die nächste der Aufgaben gemacht, welche lautet:

$$\sum _{ n=3 }^{ \infty }{ \frac { 3·{ 2 }^{ n+2 } }{ { 3 }^{ n+4 } } }$$

Wenn ich jetzt, dementsprechend angepasst, hier mit

$$\frac { { 3 }^{ -4 } }{ { { 3 }^{ -4 } } }$$ 

multiplizieren würde, geht dass doch aber leider im Zähler wegen dem n+2 nicht mehr auf oder?;)

---

Du lernst sehr schnell;-) Im Zähler kannst Du jedoch denselben Trick noch einmal verwenden mit $$\dfrac{2^{-2}}{2^{-2}}$$