Seien a, b ∈ R, a < b, und sei f : [a, b] → R konvex.

Question

Auf eure Hilfe werde ich mich freuen.

Seien a, b ∈ R, a < b, und sei f : [a, b] → R konvex.
(a) Seien x, x1, x2 ∈ [a, b] mit x1 < x < x2. Zeigen Sie, dass (f(x) − f(x1))/(x − x1) ≤ (f(x2) − f(x1))/(x2 − x1) ≤ (f(x2) − f(x))/(x2 − x).

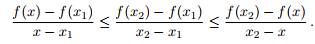
(b) Folgern Sie aus (a), dass f auf (a, b) stetig ist. Muss f auch auf [a, b] stetig sein? (Beweis oder Gegenbeispiel)
Hinweis: Zeigen Sie mit Teil (a), dass für jedes x0 ∈ (a, b) die durch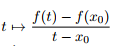  

gegebene Funktion auf [a, b] \ {x0} monoton wachsend und beschränkt ist.

 

Answer 1

Hi,

Ich zeige mal folgende Ungleichung, die andere wird genauso gehen, vermute ich. Also
$$(1) \quad \frac{ f(x) - f(x_1) }{ x - x_1 } \le \frac{ f(x_2) - f(x_1) }{ x_2 - x_1 }$$
mit $x_1 < x < x_2$ und
$x$ kann man schreiben als $x = t x_1 + (1 - t) x_2$. Das in (1) eingesetzt ergibt
$$\frac{ f(t x_1 + (1 - t) x_2) - f(x_1) }{ t x_1 + (1 - t) x_2 - x_1 } \le \frac{ f(x_2) - f(x_1) }{ x_2 - x_1 } \Leftrightarrow$$
$$\frac{ f(t x_1 + (1 - t) x_2) - f(x_1) }{ (1 - t) (x_2 - x_1) } \le \frac{ f(x_2) - f(x_1) }{ x_2 - x_1 } \Leftrightarrow$$
$$f(t x_1 + (1 - t) x_2) - f(x_1) \le (1 - t) ( f(x_2) - f(x_1) )\Leftrightarrow$$
$$f(t x_1 + (1 - t) x_2) \le (1 - t) ( f(x_2) - f(x_1) ) + f(x_1) = t f(x_1) + (1-t) f(x_2)$$
Die letzte Ungleichung ist aber gerade die Definition der Konvexität.

Das die Funktion $g(t) = \frac{ f(t) - f(x_0) }{ t - x_0 }$ monoton wachsend ist, folgt direkt aus (1)