Quadrat Flächeninhalt Konstruieren

Question

Hi,

Wie konstruiert man ein Quadrat mit dem Flächeninhalt von 7cm² wenn nichts gegeben ist?

Answer 1

Die Basis dazu könnte z.B. der Höhensatz im rechtwinkligen Dreieck sein. Sind $p$ und $q$ die Abschnitte auf der Hypotenuse, die durch den Höhenfußpunkt getrennt werden, so gilt für die Höhe $h_c$

$$h^2_c = p \cdot q$$

Die Konstruktion ginge dann so:

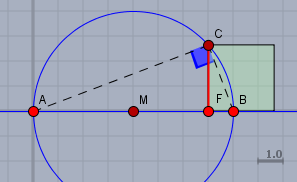
Trage auf einer Geraden die Strecke AF mit 7cm ($p$) und FB mit 1cm ab ($q$). M sei der Mittelpunkt von AB. Zeichne den Thaleskreis über AB und eine Senkrechte in F zur Geraden durch AB. Die Senkrechte schneidet den Kreis in C. Die Strecke FC ist $h_c$. Nach dem Höhensatz (s.o.) ist

$$h_c = \sqrt{p \cdot q} = \sqrt{7 \text{cm} \cdot 1\text{cm}} = \sqrt{7}\text{cm}$$

Das Quadrat zu vervollständigen sollte nun kein Problem mehr sein.

Answer 2

G=7cm²

Die Formel ist:

G=a²

also ist -----> √G=a

a=√7

a=2.65cm

Also ist jede Seite 2.65cm lang.

usw.

u=4*a

d=a*√2

r_i=a/2

r_u=a/(√2)

Answer 3

Immerhin sind Fläche (7) und Form (Quadrat) gegeben. Da kann mannicht sagen, dass nichts gegeben ist. Die Betonung liegt auf "konstruiere" und nicht "rechne" (wie bei Anton). Es geht darum, die √7 zu konstruieren. Eine Möglichkeit hat Werner genannt. Es gibt weitere. Ein Quadrat mit der Seitenlänge √7 hat die Fläche 7.

Comments

Hallo Roland,

Ich habe rechnerisch herausgefunden wie man ein Quadrat konstruiert. 

Wenn man weiß, dass alle Seiten 2.646cm lang sind sollte es wohl nicht so schwer sein es zu konstruieren?

---

"Wenn man weiß, dass alle Seiten 2.646cm lang sind ..." und wenn man es nicht weiß!? Abgesehen davon wäre es noch nicht mal exakt, sondern nur eine Näherung!

In der Aufgabe steht: 'konstruieren' und nicht 'ungefähr ausrechnen'! ;-)

---

Hier nochmal ein bisschen genauer! ;-)

Nein, jetzt mal ernhaft. Ist es nicht viel einfach 2.65cm gleiche linien aneinander zu reihen???

"und wenn man es nicht weiß!?"

Wenn der Grundflächeninhalt gegeben ist, ist es einfacher als deine Methode...

---

Hallo Antoooooon,

es geht nicht um einfach oder nicht einfach, es geht darum eine Aufgabe zu lösen. Es soll ein Quadrat konstruiert werden und auch wenn es nicht explizit da steht, es sind als Hilfsmittel nur Zirkel und Lineal erlaubt (Stichwort 'Konstruktion'). Das ist zumindest die klassische Vorgehensweise seit Euklid (bzw. mit euklidischen Werkzeugen).

Gruß Werner

---

Okay, Okay,

1:0 für Dich.

Aber in der Theorie ist es rechnerisch einfacher!

LG