integral von 1/(x2-5).

Question

$$\frac{1}{x^2-5}$$

also ich muss partial-Bruchzerlegung durchführen und danach integrieren

sowie hier:

und die Lösung ist:

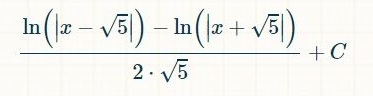
Das Integrieren am Schluss ist einfach.

Meine Frage: wie kommt diese Partialbruchzerlegung zustande?

es geht doch so:

$$\frac{a}{x-NS_1} + \frac{b}{x-NS_2}$$

$$=\frac{a}{x-√5} + \frac{b}{x+√5}$$

und nun einfach auf den selben Nenner bringen, usmultiplizieren dann LGS und a b rausfinden... a = 1, b = -1...

aber ich komm von hier nicht auf die Umgeformte Form... daher erhalte ich auch kein 2*√5 am Ende im Nenner... 

mfg.

Answer 1

1 / (x² - 5) = a / (x - √5) + b / (x + √5)

1 = a(x + √5) + b(x - √5)

Nun gilt

0 = ax + bx --> b = -a

1 = a(x + √5) - a(x - √5)

und 

1 = a*√5 + a*√5

1 = a*2*√5

a = 1 / (2*√5)

Comments

also ich komme leider immer noch nicht auf selbe hinaus
also a und b habe ich jetzt mittlerweile aber...

mein ergebis: $=\frac{ln(+x-√5)-ln(x+√5)}{2√5}$
die Lösung: $=\frac{ln(√5-x)-ln(x+√5)}{2√5}$... beim ersten ln ist ein vz fehler bei mir?



mfg

---

schon geklärt... 

danke :D

Answer 2

Meine Berechnung:

Comments

ok ich hatte ein Fehler beim koeffizientenvergleich aber dennoch komme ich nicht aufs richtige ergebnis;

mein ergebis: $=\frac{ln(+x-√5)-ln(x+√5)}{2√5}$

die Lösung: $=\frac{ln(√5-x)-ln(x+√5)}{2√5}$.. beim ersten ln ist ein vz fehler bei mir?

mfg

---

ich habe zu Ende gerechnet und komme auf das Ergebnis des Rechners:

---

keine ahnung warum wolfram so was rausgespuckt hat.. das erste ergebnis oben in der fragestellung ist genau das was ich habe...

vielen dank :D