Neuer Rechner: LGS Pro - Schrittweise Lösung von Linearen Gleichungssystemen

Question

Herzlichen Dank an Alexander Weers, der uns seinen extrem hilfreichen LGS-Rechner zur Verfügung gestellt hat. Der "LGS Pro" ist nun Teil der Assistenzrechner, was mich persönlich richtig freut! Damit erhält das Tool auch die Aufmerksamkeit, die es verdient.

LGS Pro ist der Online-Rechner zum schrittweisen Lösen von linearen Gleichungsystemen

Aufrufen: https://www.matheretter.de/rechner/lgspro

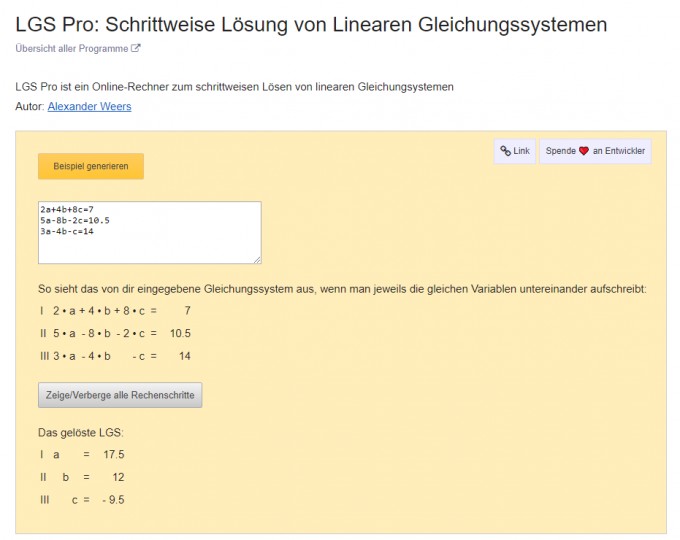
Hier eine Bildschirmaufnahme, wie schnell das Programm die LGS automatisch lösen kann:

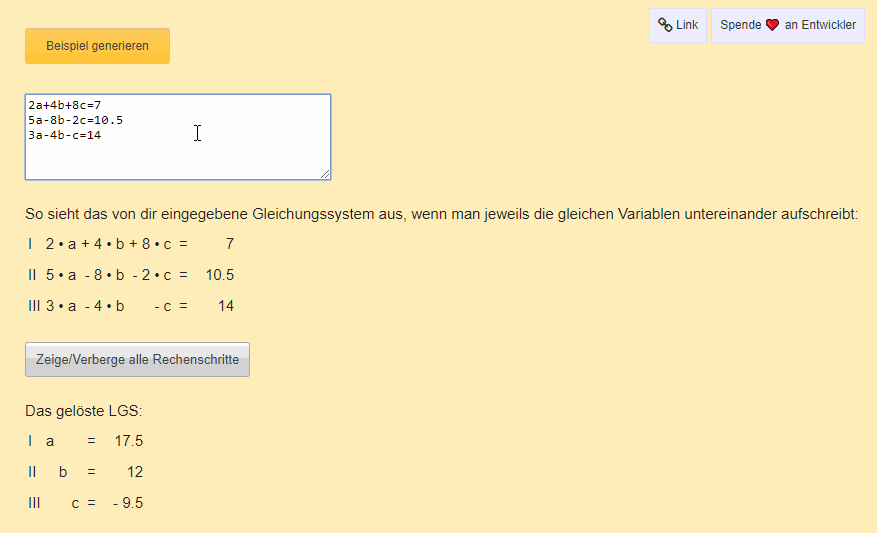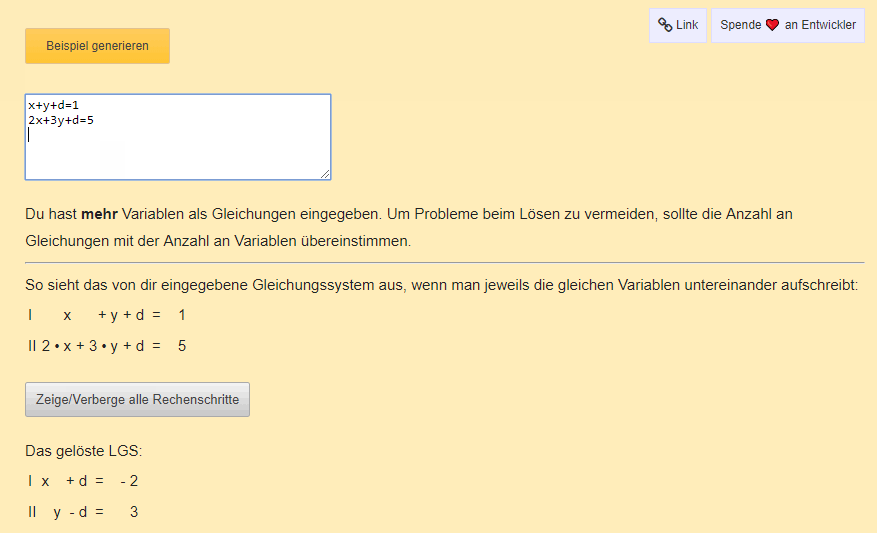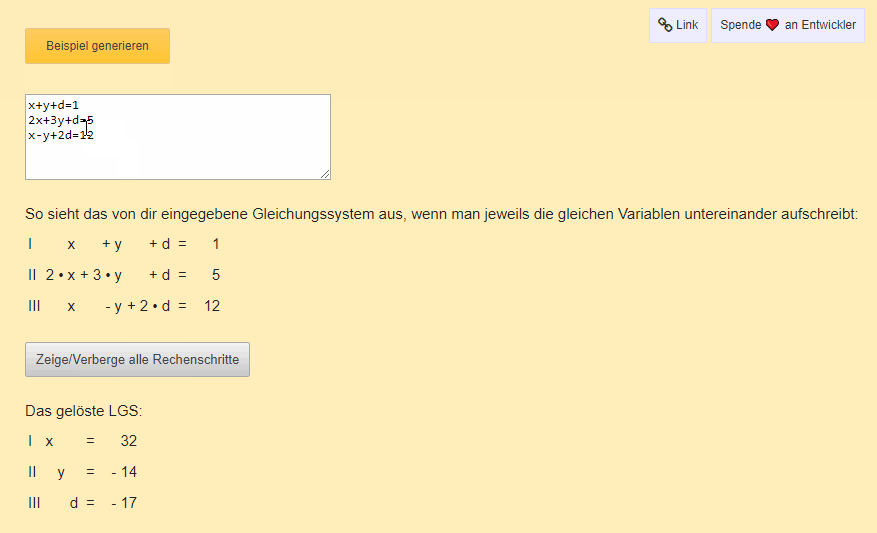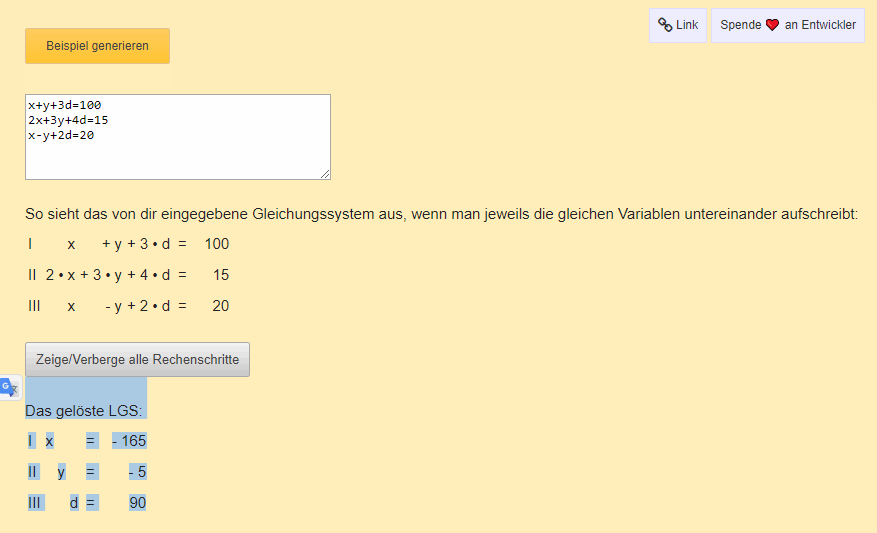
Lineare Gleichungssysteme begegnen den meisten Schülern und Studenten und bereiten Kopfzerbrechen. Die richtige Vorgehensweise bei der Lösung ist entscheidend, um Probleme zu vermeiden. Dieser Rechner ist die ultimative Hilfe für euch, denn er zeigt nicht nur die Ergebnisse, sondern beschreibt alle Rechenschritte zur Lösung des LGS. So wird die Lösung transparent und vollständig nachvollziehbar. 

Ihr könnt eine Vielzahl an Variablen eingeben! Der Rechner ist in der Lage, das LGS komplett zu lösen. 

Der LGS Pro schlägt unseren bisherigen LGS-Rechner, da man hier die Variablen frei wählen und setzen kann. Zudem zeigt er jeden einzelnen Rechenschritt an (einfach auf den Button "Zeige alle Rechenschritte" klicken). Und es gibt zahlreiche Erklärungen zu den einzelnen Schritten.

Beispiel: Erklärung der einzelnen Rechenschritte

Ihr könnt damit die meisten LGS-Aufgaben auf der Mathelounge berechnen lassen! Bzw. Berechnungen sehr schnell überprüfen (die Berechnung erfolgt sofort mit Eingabe und dauert nicht mal eine halbe Sekunde).

Viel Erfolg und Freude damit!
Kai

PS: Wer dem Entwickler übrigens spenden möchte, der kann das hier direkt tun: https://www.lgs-loesen.de

Answer 1

Prinzipiell ist der Rechner nicht schlecht. Leider arbeitet der Rechner mit Dezimalzahlen und er ist leider nicht sehr intelligent.

Bsp.

a + b = 10
7a + b = 100

Anstatt jetzt die erste Gleichung mal 7 zu nehmen wird die zweite Zeile durch 7 geteilt.

Noch schöner wäre es natürlich wenn hier das b eliminiert werden würde.

II - I

6a = 90
a = 90/6 = 15

Da mag ich meinen Schülern gar nicht die Lösung anbieten. Vor allem schreiben die das dann auch noch mit Dezimalzahlen auf und wundern sich wenn sie mit gerundeten Werten rechnen, dass am Ende nur Murks heraus kommt.

Schön wäre es wenn also die Gleichungen auf das kgV gebracht werden, indem nur mit ganzen Zahlen multipliziert wird.

a + b = 10
7a + b = 100

Also hier erste mal 7

7a + 7b = 70
7a + b = 100

I - II

6b = -30
b = -30/6 = -5

Noch schöner wäre natürlich auch noch eine intelligente Variablenelimination.

Comments

vielen Dank für Ihren Hinweis. Sie haben Recht, die Vorgehensweise des Rechner war tatsächlich (gerade für Schüler) ungünstig. Sowohl die intelligente Variablenelimination, als auch das Multiplizieren mit kleinen Brüchen (*0,167 anstelle von :6) kann zu Verwirrungen führen und das ist natürlich nicht erwünscht.

Deshalb habe ich mir Ihren Vorschlag zu Herzen genommen und eine intelligentere Variablenelimination sowie die bevorzugte Division bei Dezimalzahlen kleiner als 1 implementiert. So sollte die Nutzung auch für Schüler möglich sein.

Die Variablen werden jetzt, wie von Ihnen vorgeschlagen, auf den KGV gebracht und so werden die störenden Dezimalzahlen vermieden.

Vielen Dank für Ihr Feedback, nur so kann der Rechner besser werden!

Alexander Weers

---

Hallo Alexander.

Danke für die schnelle Umsetzung. Als Dank habe ich dir eine kleine Spende geschickt.

Demnächst werde ich sicher das Tool mit Schülern testen. 

---

zunächst erstmal vielen Dank für die Spende, ich habe mich sehr gefreut!

Sollten Ihnen oder Ihren Schülern noch etwas auf- oder einfallen, freue ich mich weiterhin über Feedback.

Liebe Grüße

---

Mir fällt da sicher etwas ein. Z.B.

I x + y + z = 6 | * 221
II 13 * x + 7 * y - z = 24 | * -17
III 17 * x + 3 * y + 2 * z = 29 | * -13

Es ist ungünstig hier alles auf einen Hauptnenner zu bringen

I x + y + z = 6
II 13 * x + 7 * y - z = 24 | II - 13*I
III 17 * x + 3 * y + 2 * z = 29 | III - 17*I

Sodass sich dann ergibt

I x + y + z = 6
II - 6·y - 14·z = -54
III - 14·y - 15·z = -73 | 3*III - 7*II

I x + y + z = 6
II - 6·y - 14·z = -54
III 53·z = 159

Ich nummeriere tatsächlich auch immer die Gleichungen mit I, II und III.

Es gibt aber Lehrer die bestehen darauf, dass die neuen Gleichungen z.B. I', II' und III' genannt werden.

Eventuell können entstehende Zeilen auch geteilt werden.

Wenn man z.B. sieht das die zweite Zeile ein Vielfaches von 2 ist.

II - 6·y - 14·z = -54
II - 3·y - 7·z = -27

Da dies aber am kgV nichts ändert würde ich es tatsächlich unterlassen.