Punktweise Konvergenz aber nicht gleichmäßige Konvergenz von Funktionenfolge f_(n)(x) = nx(1-x)^n

Question

Wie zeige ich bei folgenden Funktionenfolge, dass diese punktweise konvergiert aber nicht gleichmäßig auf dem Intervall [0,1]?

Folge: f_(n)(x) = nx(1-x)^n

Comments

Das Problem für glm Konvergenz dürfte bei x=0 liegen. Dort kommt es für zunehmende n zu immer steileren Anstiegen, während bei x=1 die Kurve ziemlich flach wird.

~plot~ x*(1-x)^{1}; 2x*(1-x)^{2};3x*(1-x)^{3};7x*(1-x)^{7};10x*(1-x)^{10} ~plot~

---

Vom Duplikat:

Titel: Punktweise und gleichmäßige Konvergenz

Stichworte: funktionenfolge,gleichmäßig

ich habe Probleme bei der Aufgabe und hoffe auf Hilfe.

Ich würde mich freuen, wenn mir es einer erklären könnte.

Aufgabe:

Wir betrachten für n ∈ ℕ die Funktion fn : [0,1] → ℝ mit fn (x) := nx(1-x)^n

Zeigen Sie, dass die Funktionenfolge (fn) für n → unendlich punktweise, aber nicht gleichmäßig gegen eine stetige Funktion

f: [0,1] → ℝ konvergiert.

Answer 1

Da es um gleichmaessige Konvergenz (nicht Stetigkeit) geht, ist -- wenn man als punktweise Grenzfunktion mal \(f=0\) annimmt (waere als erstes auszurechnen!) -- das Problem der Hubbel (Maximum) im Intervall \([0, 1]\). Der geht nicht gegen null. Zu zeigen waere also $$\sup_{x\in[0,1]}|f_n(x)|\quad\text{ist keine Nullfolge.}$$

Comments

D.h. die rel. Maxima in diesem Bereich in Abhängigkeit von n ausrechnen und dann den Grenzwert untersuchen(?)

Danke für den Hinweis. 

---

Ja, darauf laeuft es raus.

Fuer die Fragestellerin als Kochrezept:

1) Punktweise Grenzfunktion \(f(x):=\lim_{n\to\infty}f_n(x)\) für \(x\in A\) ausrechnen. (Bei den meisten Aufgaben kommt \(f=0\) raus.)

2) Die \(f_n\) konvergieren genau dann gleichmaessig in \(A\) gegen \(f\), wenn \(\sup_{x\in A}|f_n(x)-f(x)|\) eine Nullfolge ist. Das Supremum kriegt man raus, indem man eine kleine Kurvendiskussion für \(f_n-f\) macht. Das \(n\) ist der Scharparameter. Geht wie in der Schule gelernt.

---

Das hier könnte vielleicht auch noch nützlich sein, wenn die Aufgabe mal etwas anders aussieht. https://www.mathelounge.de/304312/gleichmassige-und-punktweise-konvergenz-funktionenreihen

---

Hallo, ich habe eine Frage zu deiner Vorgehensweise:

Text erkannt:

2) Die \( f_{n} \) konvergieren genau dann gleichmaessig in \( A \) gegen \( f, \) wenn \( \sup _{x \in A}\left|f_{n}(x)-f(x)\right| \) eine Nullfolge ist. Das Supremum kriegt man raus, indem man eine kleine Kurvendiskussion für \( f_{n}-f \) macht. Das \( \boldsymbol{n} \) ist der Scharparameter. Geht wie in der Schule gelernt.

 Bestimme ich quasi das Maximum von

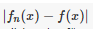 für einen Wert x, sodass ich einen Wert für x in abhängigkeit von n erhalte und schaue dann ob für diesen Wert x unter der Limesbetrachtung n gegen unendlich gegen Null konvergiert, was bei
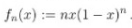 nicht der Fall sein sollte?

Gruß,

Felix

Text erkannt:

\( f_{n}(x):=n x(1-x)^{n} \)

Text erkannt:

\( \left|f_{n}(x)-f(x)\right| \)

Text erkannt:

\( \left|f_{n}(x)-f(x)\right| \)

---

Hallo Felix, warum genau denkst du, dass du hier die gleiche Frage hast, wie Sandra 2018?

Hast du die gleiche Funktionenfolge?