Hi
um den Vorzustand zu berechnen benutzt man ja das LGS!
Nun wird jedoch gesagt, dass man mithilfe der Inversen Matrix diesen Vorzustand auch berechnen kann...
Zunächst einmal die Formulierung (siehe ABB 1) und das aufgeschriebe Lösungsraster (siehe ABB 2)
Ich bin echt überfordert, da ich auch noch nicht richtig die Inverse Matrix verstanden habe...
Es ist sehr wichtig, deshalb würde ich mich sehr über Antworten freuen !  ABB 1
ABB 1
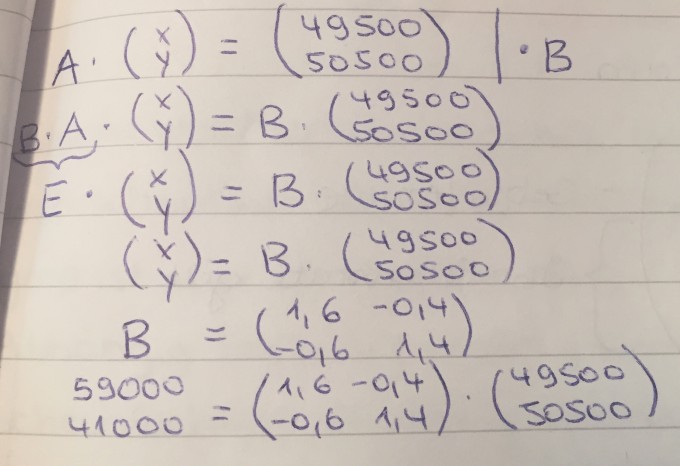 ABB 2
ABB 2