Aufgabe zur Normalverteilung

Question

Nehmen sie an, dass das Gewicht X (in Gramm) von einer zufällig ausgewählten Packung Kaffee einer bestimmten Marke normalverteilt ist mit Erwartungswert μ = 16 und Standardabweichung σ = 0.32. Wie hoch ist die Wahrscheinlichkeit, dass das Gewicht von zwei unabhängig gezogenen Packungen von dieser Marke um mehr als 0.5 Gramm abweichen? Eine Standardnormalverteilungstabelle darf benutzt werden.

Die Lösung zu dieser Aufgabe habe ich, jedoch weiß ich nicht, wie man auf den Lösungsweg kommt:

P( | X₁ − X₂ | > 0.5) ≈ 0.27

Comments

Hier eine Idee:

Du hast einen Erwartungswert von \(\mu=16\) und eine Standardabweichung von \(\sigma=0.32\) für eine Packung Kaffee. Ich halte es als sinnvol zu gucken, wie hoch die Wahrscheinlichkeit für eine Packung Kaffee ist.
Ich vermute, dass gefragt wird wie hoch die Wahrscheinlichkeit ist, dass die Packung um \(0.5g\) vom Erwartungswert abweicht, das heißt wir untersuchen das Intervall \([\mu+0.5;\mu-0.5]\). Wir haben also folgende Rechnung:$$P(15.5≤X≤16.5)=\Phi\left(\frac{16.5-16}{0.32}\right)-\Phi\left(\frac{15.5-16}{0.32}\right)$$$$P(15.5≤X≤16.5)=\Phi\left(1.56\right)-\Phi\left(-1.56\right)$$$$P(15.5≤X≤16.5)=\Phi\left(1.56\right)-(1-\Phi\left(1.56\right))$$ Nun die Werte einer Standardnormalverteilungstabelle entnehmen:$$P(15.5≤X≤16.5)=0.94062-(1-0.94062)=0.88124$$ Da wir aber alle Werte suchen, die außerhalb davon sind müssen wir noch \(1-0.88124\) rechnen, um auf \(0.11876\) zu kommen.

Die Wahrscheinlichkeit, dass zwei davon darüber sind liegt bei \(0.11876^2\)

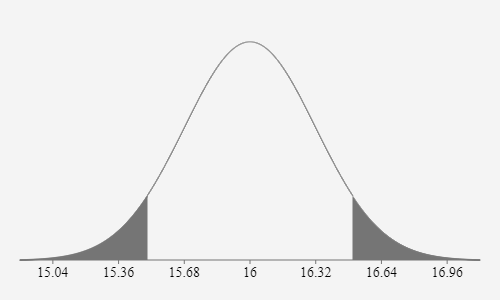
Es wurde im Prinzip folgende Wahrscheinlichkeit ausgerechnet:

---

Hallo und danke für die schnelle Antwort! Deine Rechnung kann ich so weit nachvollziehen. Aber bei meiner Aufgabe ist ja nicht die Abweichung von 0,5g vom Erwartungswert gefragt, sondern die Wahrscheinlichkeit, dass 2 zufällig und unabhängig voneinander gezogene Packungen um mehr als 0,5g voneinander abweichen. Das hat ja nicht die gleiche Bedeutung, oder? Als Lösung ist bei mir auch P( | X1 − X2 | > 0.5) ≈ 0.27 angegeben und bei dir kommt 0.11876 heraus.

---

Achso, jetzt verstehe ich die Frage erst. Die Frage ist, wie hoch die Wahrscheinlichkeit ist, dass sie voneinader um 0.5g abweichen. Dann lass mich noch mal nachdenken.

---

Hmm, spontan fällt mir nichts ein. Ich lasse die Aufgabe mal offen, in dem ich meine  Antwort in einen Kommentar umwandle.

Answer 1

Wir haben \(\mu_x=16\) und \(\mu_y=16\). Ferner haben wir \(\sigma_x=0.32\) und \(\sigma_y=0.32\). Der Gesamterwartungswert \(\mu_{x+y}\) berechnet sich wie folgt:$$\mu_{x+y}=16+16=32$$ Bei der Standardabweichung gilt:$$\sigma_{x+y}=\sqrt{0.32^2+0.32^2}=\frac{8\sqrt{2}}{25}$$ Wir berechnen nun die Wahrscheinlichkeit, dass diese Zufallsvariablen 0.5g von einander abweichen. Dazu untersuchen wir das Intervall \([\mu+0.5;\mu-0.5]\), also \([31.5;32.5]\). Dazu folgende Rechnung:$$P(31.5≤X≤32.5)=\Phi\left(\frac{32.5-32}{\frac{8\sqrt{2}}{25}}\right)-\Phi\left(\frac{31.5-32}{\frac{8\sqrt{2}}{25}}\right)$$$$P(31.5≤X≤32.5)=\Phi(1.1)-\Phi(-1.1)$$$$P(31.5≤X≤32.5)=\Phi(1.1)-(1-\Phi(1.1))$$ Werte einer Standardnormalverteilungstabelle entnehmen:$$P(31.5≤X≤32.5)=0.86433-(1-0.86433)$$$$P(31.5≤X≤32.5)=0.72866$$ Nun noch von \(1\) abziehen \(≈ 0.27134\)

Comments

Super! Vielen Dank für die Lösung:)

Könntest du mir vielleicht noch erklären, warum man hier die 2 Erwartungswerte (bzw. Standardabweichungen) addieren darf um den Gesamterwartungswert zu erhalten? Gibt es dafür einen Satz?

---

Allgemein gilt:

E(X+Y)=E(X)+E(Y)

σ₁₊₂=√(σ₁^2+σ₂^2)

---

Ah, das gilt, weil die Zufallsvariablen unabhängig sind jetzt erinnere ich mich:) :)

---

Richtisch! Nur bei unabhängigen Zufallsvariablen.