Die Anzahl \(p\) der PKWs und die Anzahl \(l\) der LKWs wird durch die Belegung in den Werkstätten begrenzt. Die Belegungszeit \(t_R\) in der Reparaturwerkstatt und die Zeit \(t_L\) in der Lakierungswerkstatt, berechnet sich aus den Anzahlen \(p\) und \(l\). Laut Aufgabenstellung ist: $$t_R = 20\text{h} \cdot p + 10\text{h} \cdot l \le 150\text{h} \\ t_L = 15\text{h} \cdot p + 20\text{h} \cdot l \le 175\text{h}$$
Diese beiden Grenzen trage ich als (blaue) Geraden in ein Koordinatensystem ein. Wobei die horizontale Achse die Anzahl \(l\) der LKWs und die vertikale Achse die Anzahl \(p\) der PKWs angibt.
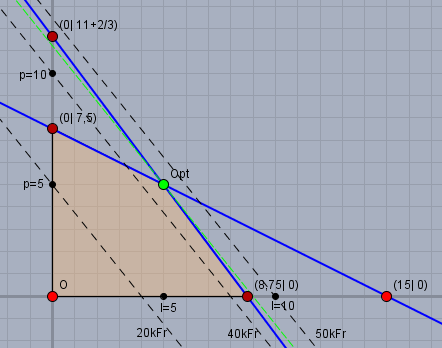
So ist z.B. mit \((l=0| \, p=7,5)\) oder mit \((l=15| \, p=0)\) die Lakierungswerkstatt mit 175h ausgelastet. Die Reparaturwerkstatt ist z.B. mit \(l=8,75| \, p=0\) oder mit \((l=0|\, p=11 \frac23)\) Fahrzeugen ausgelastet. D.h. das Ergebnis kann sich nur innerhalb der bräunlich markierten Fläche befinden (das Planungspolygon). Der Gewinn \(g\) berechnet sich nach Aufgabenstellung aus: $$g = 4000 \text{Fr} \cdot p + 5000 \text{Fr} \cdot l$$ Um das Optimum aus der Skizze ablesen zu können, habe ich Linien mit gleichem Gewinn als gestrichelte Geraden eingezeichnet. Umso mehr die Gerade sich nach rechts oben verschiebt, desto höher ist der Gewinn. Die erste Gerade, die durch den Punkt \((l=0| \, p=5)\) geht, entspricht einem Gewinn von \(20000 \text{Fr}\). Die Gewinngerade, die das Planungspolygon gerade noch berührt, haben ich grün eingezeichnet. Sie geht durch den Punkt \(Opt = (l=5|\, p=5)\) und entspricht einem Gewinn von: $$g_{\text{opt}} = 4000 \text{Fr} \cdot 5 + 5000 \text{Fr} \cdot 5 = 45000 \text{Fr}$$ Gruß Werner