Es ist mir noch nicht klar, wie ich die Koordinaten anderer Eckpunkte finden kann
Zunächst das Bild zur Aufgabe:
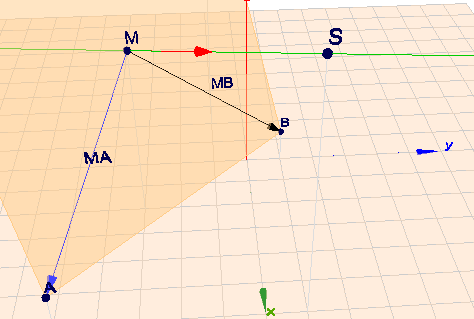
(klick auf das Bild)
Die Trägergerade (grün) der Höhe steht senkrecht auf der Grundfläche und damit auf der Ebene \(E\), in der die Grundfläche liegt. Damit ist der Richtungsvektor (2|2|1) (rot) der Geraden gleichzeitig der Normalenvektor der Ebene.
Der Punkt \(A\) liegt natürlich in der Ebene - damit kann man die Ebenengleichung in der Normalform aufstellen:$$\begin{aligned} \begin{pmatrix} 2 \\ 2\\ 1\end{pmatrix} x &= \begin{pmatrix} 2\\ 2 \\ 1 \end{pmatrix} \cdot A = \begin{pmatrix} 2\\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 6 \\ -5 \\ 1 \end{pmatrix} \\ \implies E: \space \begin{pmatrix} 2 \\ 2\\ 1\end{pmatrix} x &= 3\end{aligned}$$Der nächste Schritt besteht darin, denn Fußpunkt der Spitze \(S\) zu berechnen. Dieser ist der gleichzeitig der Mittelpunkt \(M\) der Grundfläche, da es sich um eine gerade Pyramide handelt.
Dazu bringt man Ebene und Gerade zum Schnitt, d.h. die Geradengleichung wird in die Ebenengleichung eingesetzt:$$\begin{aligned} \begin{pmatrix} 2 \\ 2\\ 1\end{pmatrix} \left( \begin{pmatrix} 6 \\ 1 \\ 7 \end{pmatrix} + t_M \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} \right) &= 3 \\ 21 + t_M \cdot 9&= 3 \\ \implies t_m &= -2 \end{aligned}$$Man erhält den Wert für \(t_m\), der den Punkt \(M\) auf der Geraden angibt:$$M = \begin{pmatrix} 6 \\ 1 \\ 7 \end{pmatrix} + (-2) \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix}$$Der dem Punkt \(A\) gegenüberliegende Punkt \(C\) ist jetzt recht leicht zu bestimmen. Wegen der Symmetrie muss gelten: $$\vec{MC} = - \vec{AC}$$dann berechnet sich \(C\) aus$$\begin{aligned} C &= M + \vec{MC} = M - \vec{MA} = M -(A - M) = 2M - A \\ &= 2 \begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix} - \begin{pmatrix} 6 \\ -5 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ -1 \\ 9 \end{pmatrix}\end{aligned}$$Da die Grundfläche quadratisch sein soll, stehen die Diagonalen senkrecht auf einander. Der Vektor \(\vec{MB}\) muss also sowohl senkrecht auf dem Normalenvektor als auch senkrecht auf \(\vec{MA}\) stehen. Hier bietet sich das Kreuzprodukt an. Vorher normieren wir noch den Normalenvektor \(n\), damit die Länge des Ergebnisses genauso lang ist, wie \(\vec{MA}\).$$\begin{aligned} B &= M + \vec{MB} = M + \frac 1{|n|} n \times \vec{MA} \\ &= \begin{pmatrix} 2 \\ -3 \\ 5 \end{pmatrix} + \frac{1}{\sqrt{2^2 + 2^2 + 1^2}}\begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} \times \begin{pmatrix} 4 \\ -2 \\ -4 \end{pmatrix} \\ &= \begin{pmatrix} 0 \\ 1 \\ 1 \end{pmatrix} \end{aligned}$$Und den letzten Punkt \(D\) berechnet man auf die selbe Weise wie \(C\):$$D = 2\cdot M - B $$ ... das schaffst Du alleine - oder?
d) Wie lauten die Koordinaten des Punktes S’, den man durch die Spiegelung der Spitze S an der Grundfläche E erhält?
Mit den Informationen von oben ist dies relativ einfach. Wir haben oben \(t_m=-2\) - d.h. man fährt \((-2)\) mal mit dem Vektor \(n\) (dem Richtungsvektor der Geraden) von \(S\) aus, um nach \(M\) zu kommen. Wenn man dies wiederholt, also nochmal mit \(-2n\) weiter läuft, so kommt man zum Spiegelbild \(S'\) von \(S\). Setze also \(t=-4\) in die Geradengleichung ein und Du erhältst \(S'\):$$S' = \begin{pmatrix} 6 \\ 1 \\ 7 \end{pmatrix} - 4 \begin{pmatrix} 2 \\ 2 \\ 1 \end{pmatrix} = \begin{pmatrix} -2 \\ -7 \\ 3 \end{pmatrix} $$Klick oben auf das Bild, dann kannst Du \(S'\) selbst im Geoknecht3D eingeben. Dann siehst Du, das dass Ergebnis sinnvoll ist.
Falls irgend etwas unklar ist, so frage bitte nach.
Gruß Werner