Tangente an eine Ellipse

Question

Aufgabe: Ermittle Gleichungen jener Tangenten an die Ellipse, die normal zur Gerade g sind

Ell: 3x^2+4y^2=336    , g: 6x+y=10

Problem/Ansatz:

… kann mir bitte jemand  die Rechenschritte erklären?

Answer 1

Die Steigung müsste ja das Reziproke vom Kehrwert sein (\(6x+y=10 \Leftrightarrow y=-6x+10\)). Also \(t(x)=\frac{1}{3}x+n\). Außerdem ist \(3x^2+4y^2=336\) umgestellt \(y=f(x)=\sqrt{\frac{336-3x^2}{4}}\)

Man könnte eventuell das GS lösen:

I. f(x)=t(x)

II. f'(x)=t'(x)

Berücksichtige dabei auch, dass die Ambiguität der Wurzel beim Umstellen der Ellipsengleichung vernachlässigt wurde und es zwei Lösungen gibt (einfach spiegeln)

Ich erhalte \(n=\frac{2\sqrt{217}}{3}\) und \(x=-8\sqrt{\frac{7}{31}}\)

Answer 2

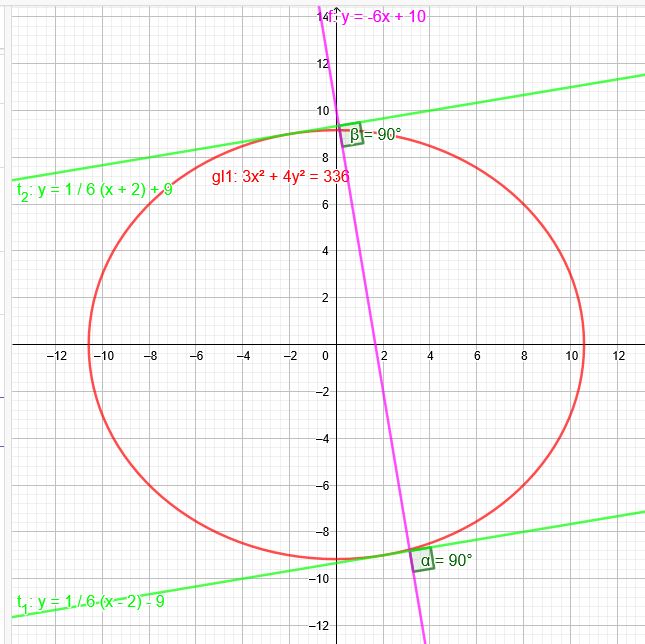
Ermittle Gleichungen jener Tangenten an die Ellipse, die normal zur Gerade g sind.
Ell: \(3x^2+4y^2=336\)       \(g: y=-6x+10\)        \(m=-6\) 

orthogonale Steigung \(m_o=\frac{1}{6} \)

\(f(x,y)=3x^2+4y^2-336\)

\(f_x(x,y)=6x\)       \(f_y(x,y)=8y\)  

\(f´(x)= -\frac{f_x(x,y)}{f_y(x,y)}\)

\(f´(x)= -\frac{6x}{8y}=-\frac{3x}{4y}\)

\(\frac{1}{6}=-\frac{3x}{4y} \)    →    \(y=-4,5x \)  

Diese Gerade schneidet die Ellipse in den gesuchten Berührpunkten:

\(3x^2+4\cdot (-4,5x)^2=336\)

\(x_1=2\)    \(y_1=-9 \)   → \(t_1: \frac{y+9}{x-2}=  \frac{1}{6} \)

\(t_1: y=\frac{1}{6}(x-2)-9 \)

\(x_2=-2\)    \(y_2=9 \)   → \(t_2: \frac{y-9}{x+2}=\frac{1}{6} \)

\(t_2: y=\frac{1}{6}(x+2)+9 \)