Aufgabe:
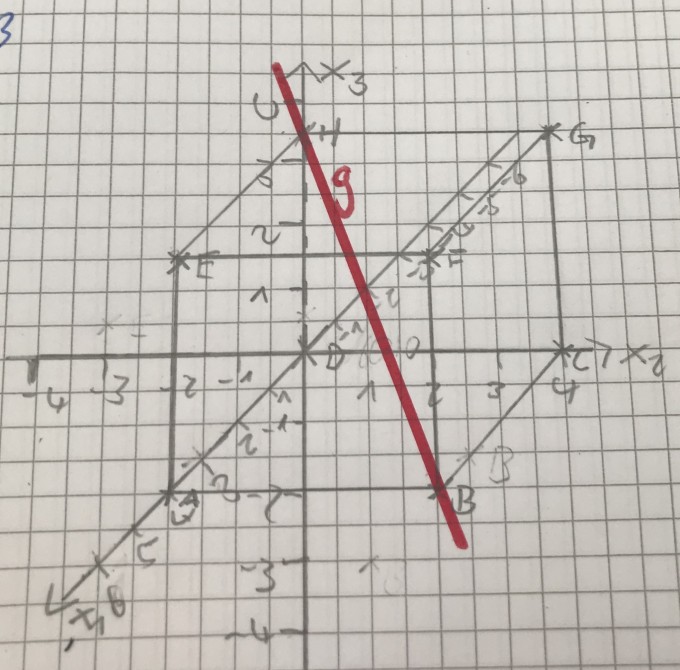
Für den Quader in Fig. 4 (Bild ist angehängt, leider etwas spärlich zu erkennen) gilt: Die Strecke AB ist 4cm lang, die Strecke BC 3cm und die Strecke AE 3,5cm lang.
a) Wählen Sie das Koordinatensystem so, dass der Punkt D im Ursprung liegt und geben Sie mögliche Koordinaten der übrigen Eckpunkte des Quaders an.
b) Geben Sie drei Gleichungen der roten Geraden g in der Parameterdarstellung an. Stützvektor soll der Ortsvektor des Punktes B sein, der Richtungsvektor sol variiert werden.
c) Welche reellen Zahlen muss man in die Gleichung von Teilaufgabe b) jeweils einsetzen, damit man die Ortsvektoren aller Punkte der Strecke BH erhält?
Problem/Ansatz:
Habe die a) gezeichnet und folgende Punkte raus: A (3|0|0), B (3|4|0), C (0|4|0), D (0|0|0), E (3|0|3,5), F (3|4|3,5), G (0|4|3,5) und H (0|0|3,5) raus. Meine erste Frage wäre ob diese Punkte richtig sind.
Sollte dies stimmen, habe ich bei der b) schon zwei Gleichungen:
1) g: Vektor x = (3|4|0) + r * (-3|-4|3,5)
2) g: Vektor x = (3|4|0) + s * (3|4|-3,5)
Da aber nur der Richtungsvektor verändert werden darf, überlege ich noch wie ich an die dritte Gleichung komme, wobei das glaube ich geht, wenn ich den Richtungsvektor so erweitere, dass er zu einem der beiden anderen kollinear ist, oder nicht?
Bei der c) bin ich leider noch etwas ratlos und bitte da gerne um Hilfe.