Regressionsgerade für transformiertes Modell zurückrechnen

Question

Aufgabe:

a) Es wird vermutet, dass zwischen dem Verkaufspreis und der Absatzmenge ein
funktionaler Zusammenhang der Form $y = a x ^ { b }$

existiert. Transformieren Sie das Modell auf ein lineares Modell der Form $v = c u + d$.

b) Für die transformierten Daten erhält man folgende Tabelle

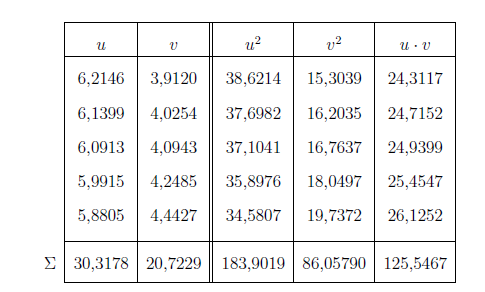
Bestimmen Sie zunächst durch eine Regression die Parameter c, d für das
transformierte Modell und hieraus die Parameter a,b.

Problem/Ansatz:

Wie erhalte ich nun a(Dach) und b(Dach) ? Wie geht die Rückrechnung genau? Es wäre sehr nett, wenn mir jemand weiterhelfen könnte. Vielen Dank im Voraus.

Euer Max

Comments

Habe heraus gefunden, dass e^d(Dach) = a(Dach) ist, also c und d haben die Plätze getauscht, so wie es ausschaut...

Answer 1

Hallo Max,

Wie Du das $c$ und $d$ aus den Daten von $u_i$ und $v_i$ berechnest. sollte Dir ja bekannt sein. Ich bekomme$$c \approx -1,581 \\ d \approx 13,731$$Aus der Exponentialgleichung folgt$$\begin{aligned} y &= a\,x^b && \left|\, \ln \right.\\ \ln(y) &= \ln(a \cdot x^b) \\ \ln(y) &= \ln(a) + \ln(x^b) \\ \ln(y) &= \underbrace{b}_{=c} \cdot \ln(x) + \underbrace{\ln(a)}_{=d} \end{aligned}$$Daraus folgt$$b = c \approx -1,581 \\ \ln(a) = d \\ a = e^{d} \approx 918693$$Folglich lautet das Modell$$y = 918693 \cdot x^{-1,581}$$

Plotlux öffnen

f₁(x) = 918693·x^(-1,581)P(500|50)P(464|56)P(442|60)P(400|70)P(358|85)Zoom: x(300…600) y(-10…100)

Gruß Werner