Intervalle auf der x-Achse in denen der Graph der Funktion oberhalb der x-Achse verläuft? h: x → x(x²-4)

Question

Aufgabe:  bestimme die Intervalle auf der x-Achse in denen der Graph der Funktion oberhalb der x-Achse verläuft

a) h: x → x(x²-4)
Problem/Ansatz:

wie berechne ich die intervalle auf der x achse und sind intervalle dasselbe wie der wertebereich,falls nicht wie würde man sowas berechnen

Answer 1

x(x²-4)=x(x-2)(x+2)

Vorzeichenwechsel bei x=-2; x=0 und x=2.

Für x<-2, z.B. x=-3

             h(-3)=-3·(-5)·(-1)=-15<0 unterhalb der x-Achse.

Für -2<x<0, z.B. x=-1

           h(-1)=-1·(-3)·1=+3>0 oberhalb der x-Achse

Für 0<x<2, ...

Für x>2, ...

Answer 2

wie berechne ich die intervalle auf der x achse
Was soll das sein? die Nullstellen
f ( x ) = x * ( x^2 - 4 )
Nullstellen f ( x ) = 0
Satz vom Nullprodukt anwenden
x = 0
und
x^2 - 4 = 0
x^2 = 4

x = -2
und
x = +2

Intervalle
-∞ bis -2
-2 bis 0
0 bis +2
+2 bis +∞

Answer 3

a) h: x → x(x²-4)
Problem/Ansatz:

wie berechne ich die intervalle auf der x achse und 

sind intervalle hier dasselbe wie der wertebereich,falls nicht wie würde man sowas berechnen

Nein. Intervalle auf der x-Achse sind Teile des Definitionsbereichs der Funktion f.

h: x ↦ x(x²-4)

Der Zuordnungspfeil ↦ zeigt an, dass einem x-Wert des Definitionsbereichs als Funktionswert x(x^2-4) zugeordnet wird.

h: x ↦ x(x²-4)

Kannst du auch schreiben als

h: x ↦ y= x(x²-4)

oder

h(x):= x(x²-4)

Den Wertebereich von h liest man auf der y-Achse ab, wenn h in einem Koordinatensystem mit horizontaler x-Achse und vertikaler y-Achse gezeichnet wird.

~plot~ x*(x^2-4) ~plot~

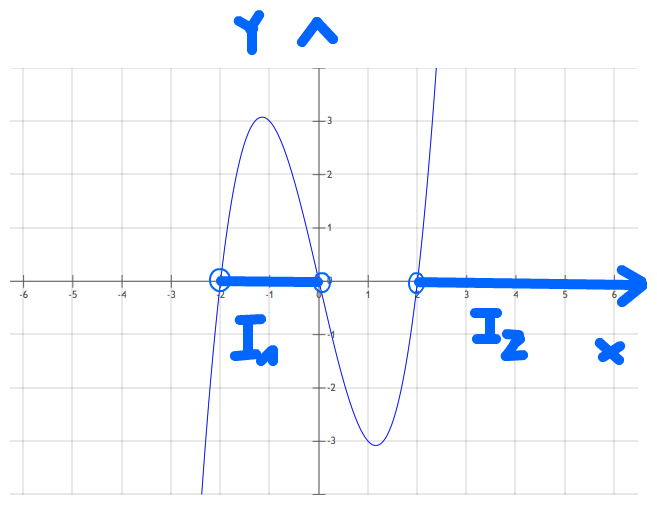
Die beiden Intervalle auf der x-Achse, in denen der Graph von h oberhalb der x-Achse verläuft, sind

I_{1} = ]-2,0[  und I_{2} = ]2,∞[ .