Hallo Anna,
Vorweg eine Bitte: teile mir doch bitte mit, ob und wie Dir die Geoknecht3D-Szenen, die ich teilweise meinen Antworten an Dich hinzu gefügt habe, weiter helfen.
Zur Aufgabe:
dann habe ich
-2=-r+s
-3=r-s
1=r+s
dann hast Du wahrscheinlich das \(r\) und das \(s\) der zweiten Gleichung nicht gegen zwei neue Buchstaben - z.B. \(u\) und \(v\) ausgetauscht. Diese Parameter (hier \(r\) und \(s\)) beziehen sich immer nur auf die lokale Ebene und sind i.a. verschieden für zwei verschiedene Ebenen. Das Gleichsetzen der Ebenen geschieht somit wie folgt:$$\begin{aligned} E_1 &= E_2 \\ \begin{pmatrix}1\\ 0\\ 3\end{pmatrix} + \begin{pmatrix}1\\ 0\\ 0\end{pmatrix}r + \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}s &= \begin{pmatrix}2\\ 3\\ 2\end{pmatrix} + \begin{pmatrix}0\\ 1\\ 1\end{pmatrix}\colorbox{#ffff00}u + \begin{pmatrix}2\\ 0\\ 1\end{pmatrix} \colorbox{#ffff00} v \\ \begin{pmatrix}1\\ 0\\ 0\end{pmatrix}r + \begin{pmatrix}1\\ 1\\ 0\end{pmatrix}s - \begin{pmatrix}0\\ 1\\ 1\end{pmatrix}\colorbox{#ffff00}u - \begin{pmatrix}2\\ 0\\ 1\end{pmatrix} \colorbox{#ffff00} v &= \begin{pmatrix}2\\ 3\\ 2\end{pmatrix} - \begin{pmatrix}1\\ 0\\ 3\end{pmatrix} \end{aligned} \\$$Das ist ein Gleichungssystem mit vier Unbekannten und drei Gleichungen. Also im Grunde eine Unbekannte zu viel. Aber das ist ja auch das, was wir erreichen wollen, da eine Gerade immer mit einem freien Parameter (hier \(t\)) versehen ist. Und dieser freie Parameter der Geraden ist quasi die übrig gebliebene Unbekannte.
Da wir hier viele 0'en bei den Koordinaten vorfinden, ist es mit einer geschickten Auswahl schnell gelöst. Setze \(v= t\) (das ist jetzt unser freier Parameter), dann folgt aus der letzten der drei Gleichungen oben$$- u - t = 2 -3 \implies u = 1 - t$$und das reicht bereits für eine Lösung, da wir nur für eine der beiden Ebenen die Parameter (hier \(u\) und \(v\)) in Abhängigkeit von \(t\) bestimmen müssen. Einsetzen in \(E_2\) gibt bereits die Schnittgerade \(g\):$$g: \space x = \begin{pmatrix}2\\ 3\\ 2\end{pmatrix} + \begin{pmatrix}0\\ 1\\ 1\end{pmatrix} (1-t) + \begin{pmatrix}2\\ 0\\ 1\end{pmatrix} t = \begin{pmatrix}2\\ 4\\ 3\end{pmatrix} + \begin{pmatrix}2\\ -1\\ 0\end{pmatrix} t$$und oh Wunder; es ist die Lösung Deines Lehrers.
Ich habe Dir das auch im Geoknecht3D eingegeben, was die Richtigkeit der Lösung bestätigt
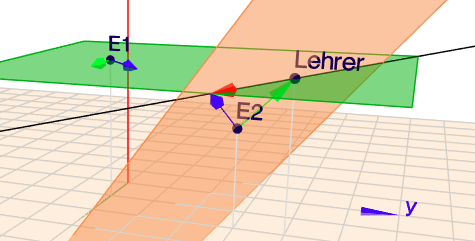
(klick auf das Bild)
Wenn Du genau hinschaust, so siehst Du, dass sich der rote Richtungspfeil der Schnittgeraden aus der Differenz der beiden Richtungsvektoren von \(E_2\) zusammen setzt. Ist $$E_2: \space x = p_2 + a \cdot u + b \cdot v$$so ist die Gerade wegen \(u=1-t\)$$g: \space x = p_2 + a \cdot (1-t) + b \cdot t = (p_2 + a) + (b-a) t$$und das kannst Du sehr schön in dem Bild oben sehen. \(a\) ist der grüne Vektor in \(E_2\) und \(b\) der blaue.
Falls Du da Fragen zu hast, so melde Dich bitte.