Hallo Totonka,
Ich habe die Ellipsengleichung: ... bewiesen.
Dann leite sie implizit ab, extrahiere \(y'\) und setzte das in die Punkt-Richtungsform einer linearen Funktion für die Tangente \(t\) ein: $$\begin{aligned} \frac{x^2}{c^2} + \frac{y^2}{d^2} &= 1 \\ \frac{2x}{c^2} + \frac{2yy'}{d^2} &= 0 \\ \implies y' &= -\frac{xd^2}{yc^2} \\ t: \space y &= -\frac{x_1d^2}{y_1c^2}(x - x_1) + y_1 && \left|\, \cdot \frac{y_1}{d^2} \right. \\ \frac{yy_1}{d^2} &= -\frac{xx_1}{c^2} + \underbrace{\frac{x_1^2}{c^2} + \frac{y_1^2}{d^2}}_{=1} &&\left|\, + \frac{xx_1}{c^2} \right. \\ \frac{xx_1}{c^2} + \frac{yy_1}{d^2} &= 1\end{aligned}$$Die 'nützlichen' Funktionen kommen zum Einsatz, wenn Du zunächst nach \(y\) und/oder \(x\) umformst und dort ableitest. Das ist aber nicht nötig. Siehe auch hier.
Das ganze kann man auch geometrisch zeigen:
Die Gleichung $$\frac{xx_1}{c^2} + \frac{yy_1}{d^2} = 1$$ist eine Geradengleichung in der Achsenabschnittsform mit den Achsenabschnitten $$x_0 = \frac{c^2}{x_1}, \quad y_0= \frac{d^2}{y_1}$$Zumindest ersteres soll im folgende gezeigt werden:
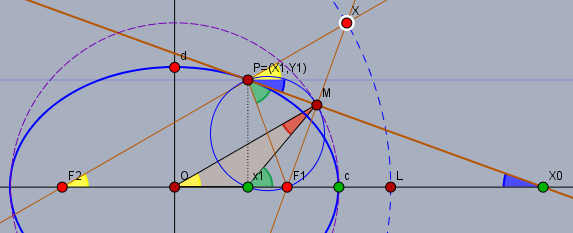
Die Tangente (braun) an die Ellipse \(E\) durch \(P=(x_1;y_1)\) kann konstruiert werden, indem man eine Gerade durch \(F_2\) und \(P\) zeichnet, die den Kreis mit Mittelpunkt \(F_2\) und Radius \(2c\) in \(X\) schneidet. Die Mittelsenkrechte der Strecke \(XF_1\) ist die Tangente \(t\) an \(E\) durch \(P\). \(t\) schneidet die X-Achse in \(X_0\). Die X-Koordinate von \(P\) ist im Punkt \(X_1\) aufgetragen.
Der Winkel \(\angle F_1F_2P\) sei \(\alpha\) (gelb) und der Winkel \(\angle MX_0O\) sei \(\beta\) (blau). Die Strecke \(|OM|\) ist die Mittelparallele des Dreiecks \(\triangle F_2F_1X\), d.h. \(|OM| = \frac 12|F_2X| = c\). Ebenso folgt daraus, \(\angle F_1OM = \alpha\) (gelb).
Das Viereck \(X_1F_1MP\) ist ein Sehnenviereck, da die Winkel bei \(X_1\) und \(M\) rechte sind. Folglich sind die Winkel \(\angle F_1X_1M\) und \(\angle F_1PM\) (beide grün) gleich groß. \(\angle F_1PM\) ist aber wegen der Symmetrie an \(t\) (Mittelsenkrechte) gleich der Summe \(\alpha + \beta = \angle MPX\). Damit ist der Winkel \(\angle OMX_1 = \beta\) (rot) wegen der Winkelsumme in \(\triangle OX_1M\).
Aus der Gleichheit der Winkel \(\angle MX_0O = \beta\) (blau) und \(\angle OMX_1\) (rot) folgt, dass das Dreieck \(\triangle MOX_1\) ähnlich zu \(\triangle OX_0M\) ist. Somit ist$$\frac {|OX_0|}{|OM|} = \frac{x_0}{c} = \frac {|OM|}{|OX_1|} = \frac {c}{x_1} \\ \implies x_0 = \frac{c^2}{x_1}$$zu zeigen, dass \(y_0 = d^2/y_1\) ist, sollte mit der Vorlage jetzt kein Problem sein.
Gruß Werner