Nullstellen, lokale Minima und lokale Maxima von ƒ

Question

Aufgabe:

Sei ƒ : ℝ → ℝ mit ƒ(x) = \( \frac{x^2}{\exp(x)} \)

a) Bestimmen Sie alle Nullstellen, lokalen Minima und lokalen Maxima von ƒ

b) Bestimmen Sie lim_x→∞ ƒ(x).

c) Erstellen Sie eine qualitative Skizze des Graphen von ƒ.

Problem/Ansatz:

Ich weiß nicht wie ich hier am besten vorgehe. Könnte mir vielleicht jemand erklären wie man die Aufgabe löst?

Answer 1

a)

$$\text{Da } e^x>0 \ \forall x\in \mathbb{R} \text{ lässt sich die einzige Nullstelle bei } x=0 \text{ finden.} \\ \text{Die Funktion f ist (n-mal) differenzierbar auf }\mathbb{R} \text{.} \\ \text{Es gilt } f'(x)=\frac{x(2-x)}{e^{x}} \text{ nach der Quotientenregel.} \\ \text{Mit } e^x>0 \text{ lässt sich } f'(x)=0 \text{ nur für } x=0 \text{ oder } x=2 \text{ realisieren.} \\ \text{Es ist } f''(x)=\frac{x^2-4x+2}{e^x} \text{ nach der Quotientenregel.} \\ \text{Es gilt } f''(0) = 2 > 0 \text{ und } f''(2)=-\frac{2}{e^2} < 0 \text{.} \\ \text{Damit gibt es ein lokales Minimum bei } x=0 \text{ und ein lokales Maximum bei } x=2 \text{.}$$

b)

$$\text{Mit L'Hospital gilt } \lim_{x\to \infty} f(x) = \lim_{x\to \infty} \frac{x^2}{e^x} = \lim_{x\to \infty} \frac{2x}{e^x} = \lim_{x\to \infty} \frac{2}{e^x} = 0 \in [-\infty, \infty] \text{.}$$

c)

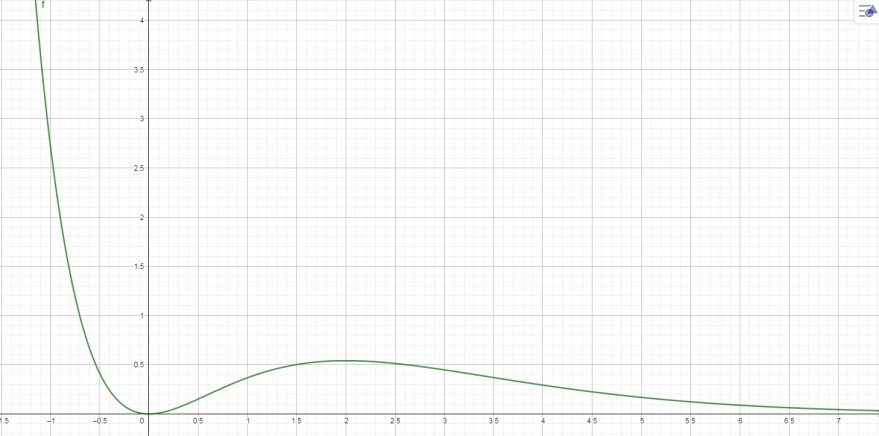
Zumindest die Nullstelle, die lokalen Maxima und Minima, sowie den Verlauf für x gegen unendlich kannst du gut einzeichnen. Im Intervall [-1.5,7.5] sieht der Graph z.B. wie folgt aus:

Comments

Dankeschön!! Du bist meine Rettung!

Answer 2

Nenner null setzen gibt die Nullstellen. Erste Ableitung null setzen gibt Extremwerte. Kontrolle über zweite Ableitung.

\(\exp(x) \)  steigt schneller als \( x^2\) deshalb geht die Funktion gegen 0 für x gegen unendlich.

Comments

Hallo Ulli,

du meinst bestimmt den Zähler.

:-)

---

Ja klar. Sorry