Ganzrationale Funktion f mit den angegebenen Eigenschaften

Question

Aufgaben:

7. Bestimmen Sie die ganzrationale Funktion $\mathrm{f}$ mit den angegebenen Eigenschaften.
a) Grad 2, Extremum bei $x=1,$ Achsenschnittpunkte bei $P(0 \mid-3)$ und $Q(5 \mid 0)$
b) Grad 4, Sattelpunkt im Ursprung, Tiefpunkt $\mathrm{P}(-2 \mid-6)$

Answer 1

Hallo Hattice,

wenn du dir meine Ausführungen zu der Aufgabe 3, die ich beanwortet habe, zu Gemüte geführt hast, solltest du wissen:

Funktion mit dem Grad 2

$$f(x)=ax^2+bx+c\\f'(x)=2ax+b$$

Extremum bei x = 1

f'(1) = 0

Q (5 | 0)

Nullstelle bei x = 5

Jetzt etwas Neues:

P (0 | -3)

Der Schnittpunkt mit der y-Achse ist bei -3, das heißt f(0) = -3

Jetzt hast du wieder drei Gleichungen...

Gruß, Silvia

Comments

Wie muss ich das jetzt mit den 3 Gleichungen machen ? Ich Blick da irgendwie nicht durch ... :(

---

So etwas nennt man dann "Gleichungssystem".

Das musst du (nicht wir) dann lösen.

---

Wie sehen deine Gleichungen denn aus?

Answer 2

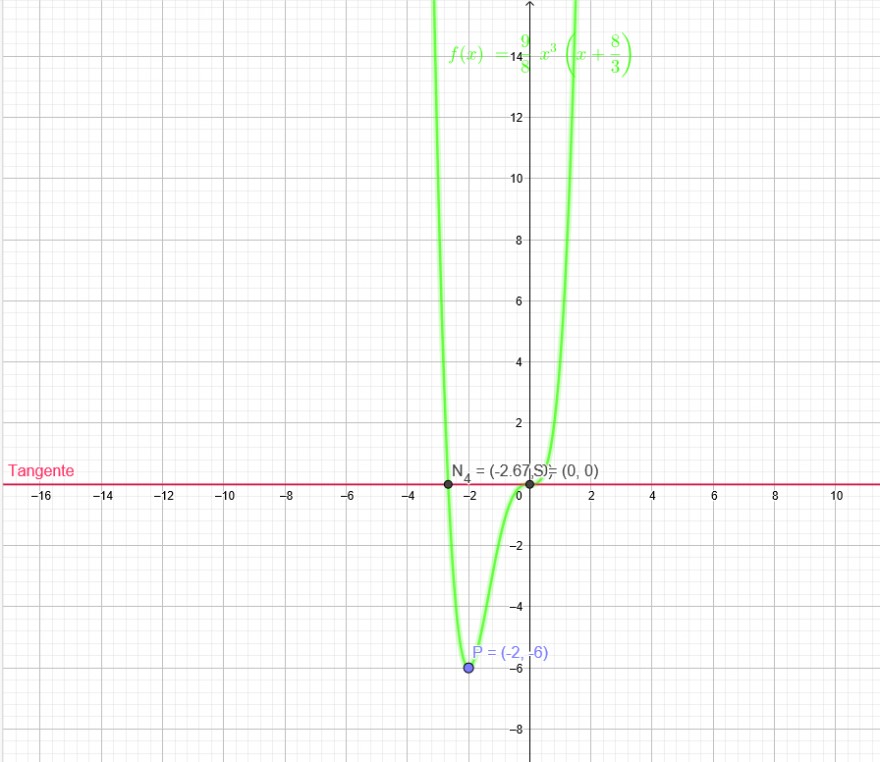
b)  Grad 4,   Sattelpunkt im Ursprung und Tiefpunkt P(-2|-6)

f(x)=a*(x-N1)*(x-N2)*(x-N3)*(x-N4)

Sattelpunkt im Ursprung:

f(x)=  a *   x³* ( x - N4 )

P(-2|-6)

f( - 2 ) = - 8  a ( -2 - N4 )

- 8  a (  - 2  - N 4  ) = - 6

4  a (  - 2  - N 4  ) =3

a  =  $\frac{3}{4 ( - 2 - N 4 ) }$

f (  x )   =  $\frac{3}{4 ( - 2 - N 4 ) }$*  [   $x^{3}$  * ( x - N4 )]

f ´  (  x )  = $\frac{3}{4 ( - 2 - N 4 ) }$*[3* $x^{2}$* ( x - N4 )+$x^{3}$*1]

f ´  (  -2  )  = $\frac{3}{4 ( - 2 - N 4 ) }$*[3* $(-2)^{2}$* (-2 - N4 )+$(-2)^{3}$]

$\frac{3}{4 ( - 2 - N 4 ) }$*[ 12* (-2 - N4 )  - 8  ]  = 0

[ 12* (-2 - N4 )  - 8  ]  = 0

N4= - $\frac{8}{3}$

a= $\frac{9}{8}$

f ( x  )   =   $\frac{9}{8}$   *   x^3   *  ( x +   $\frac{8}{3}$  )

mfG

Moliets