Beispiel - Komplexe Diff'barkeit nachweisen

Question

Aufgabe:

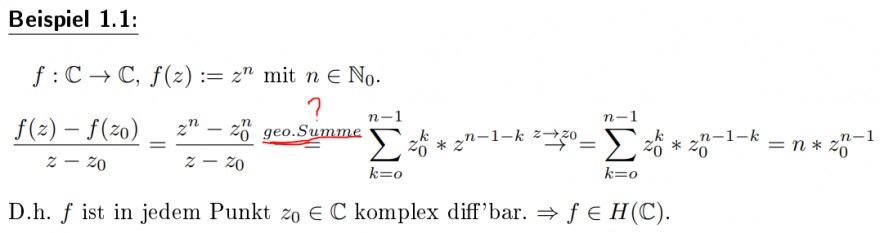
Text erkannt:

Beispiel
1.1:
$f: \mathbb{C} \rightarrow \mathbb{C}, f(z):=z^{n}$ mit $n \in \mathbb{N}_{0}$
$\frac{f(z)-f\left(z_{0}\right)}{z-z_{0}}=\frac{z^{n}-z_{0}^{n}}{z-z_{0}} \frac{\text {geo.Summe}}{=} \sum \limits_{k=o}^{n-1} z_{0}^{k} * z^{n-1-k} \stackrel{z \rightarrow z_{0}}{\longrightarrow}=\sum \limits_{k=0}^{n-1} z_{0}^{k} * z_{0}^{n-1-k}=n * z_{0}^{n-1}$
D.h. $f$ ist in jedem Punkt $z_{0} \in \mathbb{C}$ komplex diff'bar. $\Rightarrow f \in H(\mathbb{C})$.

Text erkannt:

$\frac{f(z)-f\left(z_{0}\right)}{z-z_{0}}=\frac{z^{n}-z_{0}^{n}}{z-z_{0}} \frac{\text {geo.Summe}}{=} \sum \limits_{k=o}^{n-1} z_{0}^{k} * z^{n-1-k} \stackrel{z \rightarrow z_{0}}{\longrightarrow}=\sum \limits_{k=0}^{n-1} z_{0}^{k} * z_{0}^{n-1-k}=n * z_{0}^{n-1}$

Problem/Ansatz:

, ich lerne gerade für die mündliche in Funktionentheorie und mir ist dieses Gleichheitszeichen nicht ganz klar - bzw. weiß ich nicht wie hier die Geometrische Summe einfließt - kann mir hier jemand weiterhelfen?

Answer 1

$$\frac{ z^n - z_0^n }{ z - z_0 } = \frac{ z^n }{ z } \frac{ 1 - \left( \frac{z_0 }{ z } \right)^n } { 1 - \frac{ z_0 }{ z } }$$ und jetzt die Formel für die geometrische Reihe anwenden.