Bestimmen Sie k∈ℝ so, dass die von den Graphen der Funktionen f und g eingeschlossenen Fläche den Flächeninhalt A hat.

Question

Aufgabe:

Bestimmen Sie k∈ℝ so, dass die von den Graphen der Funktionen f und g eingeschlossenen Fläche den Flächeninhalt A hat. Fertigen Sie dazu eine Skizze an und erläutern Sie daran den Einfluss des Parameters k.

b)f(x)=x² und g(x)= -x²+k

Problem/Ansatz:

Also die Nullstellen habe ich schon Ausgerechnet. X1=-Wurzel von k÷2

Und X2= + Wurzel von k÷2

Dann habe ich die Stammfunkion gebildet: -2/3x³+kx

Aber beim einsetzen der Wurzeln kommt ich einfach nicht mehr weiter. Ich hoffe mir kann jemand weiterhelfen

Comments

Absolut mein Fehler :(

Hab vergessen zu schreiben, dass A=1 sein soll.

Answer 1

d(x) = g(x) - f(x) = (k - x²) - (x²) = k - 2·x² = 0 --> x = ± √(k/2)

A = 2·∫(k - 2·x², x, 0, √(k/2)) = 1 --> k = 3^(2/3)/2 = 1.040041911

Comments

Vielen Dank, aber wie ist denn der Weg dahin? Irgendwiw verstehe ich das mit $\sqrt{k÷2}$ nicht

---

Du müsstest die Gleichung

k - 2·x² = 0

schon lösen. Das ist eine rein quadratische Gleichung und kann damit direkt nach x aufgelöst werden.

---

Wie ich nach dem x auflöse,weiß ich schon. Ich habe auch für x=±√(k/2) raus. Aber danach verstehe ich leider nix mehr. Theoretisch muss ich doch dann ±√(k/2) einmal als obere Grenze und einmal als untere Grenze nehmen. Da die Funktion quadratisch ist,reicht es ja,wenn ich +√(k/2) in die Stammfunkion einsetze und dann ×2. Sprich: 2·∫(-2·(√k/2)²+k) oder? Aber wie geht das denn ? Ich muss, da ich es mit ausführlichem Rechenweg machen muss in die Stammfunkion einsetzen. Also : 2·(-2/3·(√k/2)³+k·(√k/2))-0

Wie rechne ich sowas denn aus :(

Ich hoffe ich stelle mich nicht zu dumm an,aber ich verstehe gerade nix mehr

---

Genau

D(√(k/2)) = k·√(k/2) - 2/3·√(k/2)³
D(√(k/2)) = k·(k/2)^(1/2) - 2/3·(k/2)^(3/2)
D(√(k/2)) = 2·k/2·(k/2)^(1/2) - 2/3·(k/2)^(3/2)
D(√(k/2)) = 2·(k/2)^(3/2) - 2/3·(k/2)^(3/2)
D(√(k/2)) = (2 - 2/3)·(k/2)^(3/2)
D(√(k/2)) = 4/3·(k/2)^(3/2)

2·D(√(k/2)) = 1
8/3·(k/2)^(3/2) = 1
(k/2)^(3/2) = 3/8
k/2 = (3/8)^(2/3) = 1/4·3^(2/3)
k = 1/2·3^(2/3) = 1.040041911

---

Genau das war, wo meine Schwierigkeiten waren. Vielen vielen Dank!!

---

Könnte mir jemand erklären wie man auf (2-2/3) durch 2*(k/2)^(3/2) kommt?

PS: Letzter Kommentar von ,,der Mathecoach“ , ab der vierten D(k/2) Gleichung

---

Im folgenden hatte ich nur den gemeinsamen Faktor ausgeklammert. Ich habe das mal farbig hervorgeheben. Lag hier das Problem? Ansonsten poste mal genau die zwei zeilen, bei denen du den Übergang nicht nachvollziehen konntest.

D(√(k/2)) = 2·(k/2)^(3/2) - 2/3·(k/2)^(3/2)

D(√(k/2)) = (2 - 2/3)·(k/2)^(3/2)

---

Ok danke habe es jetzt verstanden. Frohe Weihnachten

---

Hallo, ich schreibe nächsten montag eine klausur und übe gerade und habe auch diese aufgabe mir vorgenommen zu rechnen. Ich kann diese Lösung nur teilweise nachvollziehen, ganz davon abgesehen dass es kaum leserlich für mich ist in diesem format. ist es möglich mir eine kurze ergänzung zu liefern? LG

---

Ich kann diese Lösung nur teilweise nachvollziehen, ganz davon abgesehen dass es kaum leserlich für mich ist in diesem format.

Noch mal ausführlich:

Die Schnittstellen sind$$\begin{aligned} f(x_1)&=g(x_1) \\ x_1^2 &= -x_1^2 + k &&|\, +x_1^2 \\ 2x_1^2 &= k &&|\, \div 2 \\ x_1^2 &= \frac{1}{2}k &&|\, \sqrt{} \\ x_1 &= \pm \sqrt{\frac{k}{2}} \end{aligned}$$Zur Berechnung der Fläche muss nun zwischen den Schnittstellen das Integral der Differenz $g-f$ berechnet werden:$$\begin{aligned} A &= \int\limits_{-\sqrt{\frac{k}{2}}}^{\sqrt{\frac{k}{2}}} \left(g(x)-f(x)\right)\,\text{d}x \\ &= \int\limits_{-\sqrt{\frac{k}{2}}}^{\sqrt{\frac{k}{2}}} -x^2+k-x^2\,\text{d}x \\ &= \int\limits_{-\sqrt{\frac{k}{2}}}^{\sqrt{\frac{k}{2}}} -2x^2+k\,\text{d}x \\ &= \left[-\frac{2}{3}x^3 + kx\right]_{-\sqrt{\frac{k}{2}}}^{\sqrt{\frac{k}{2}}} \\ &= -\frac{2}{3}\left(\sqrt{\frac{k}{2}}\right)^3 + k \sqrt{\frac{k}{2}} -\left(-\frac{2}{3}\left(-\sqrt{\frac{k}{2}}\right)^3 - k \sqrt{\frac{k}{2}}\right) \\ &= -\frac{4}{3}\left(\sqrt{\frac{k}{2}}\right)^3 + 2k \sqrt{\frac{k}{2}} \\ &= \left(-\frac{4}{3}\cdot \frac{1}{2} + 2\right)\sqrt{\frac{1}{2}}\,k^{\frac{3}{2}} \\ &= \frac{4}{3}\sqrt{\frac{1}{2}}\,k^{\frac{3}{2}}\\ \end{aligned}$$Und da $A=1$ sein soll, wird dann $k$ zu:$$\begin{aligned} A &=\frac{4}{3}\sqrt{\frac{1}{2}}\,k^{\frac{3}{2}} = 1 \\ \implies k^{\frac{3}{2}} &= \frac{3}{4}\sqrt{2} \\ k &= \left(\frac{3}{4}\sqrt{2}\right)^{\frac{2}{3}} \approx 1,04 \end{aligned}$$

---

Ich hab lange gebraucht um es verstehen zu können, aber das hat mir auch nochmal sehr geholfen, vielen vielen lieben dank!!!

Answer 2

f(x)=x² und g(x)= -x²+k

x²= -x²+k

2x²=k

x²=  0,5k

x_1= $\sqrt{0,5k}$

x_2= - $\sqrt{0,5k}$

A=   2* $\int\limits_{0}^{0,5k}$ [g(x)-f(x)]*dx

A=  2* $\int\limits_{0}^{0,5k}$ [-x^2+k-x^2]*dx=  2* $\int\limits_{0}^{0,5k}$ [-2x^2+k]*dx = - 4/3x^3+2 k*x

Obere Grenze 0,5k einsetzen : - 4/3*(0,5k)³+ 2 k* 0,5k = k²-0,166667k³

Untere Grenze ergibt 0

A= k²-0,166667k³

mfG

Moliets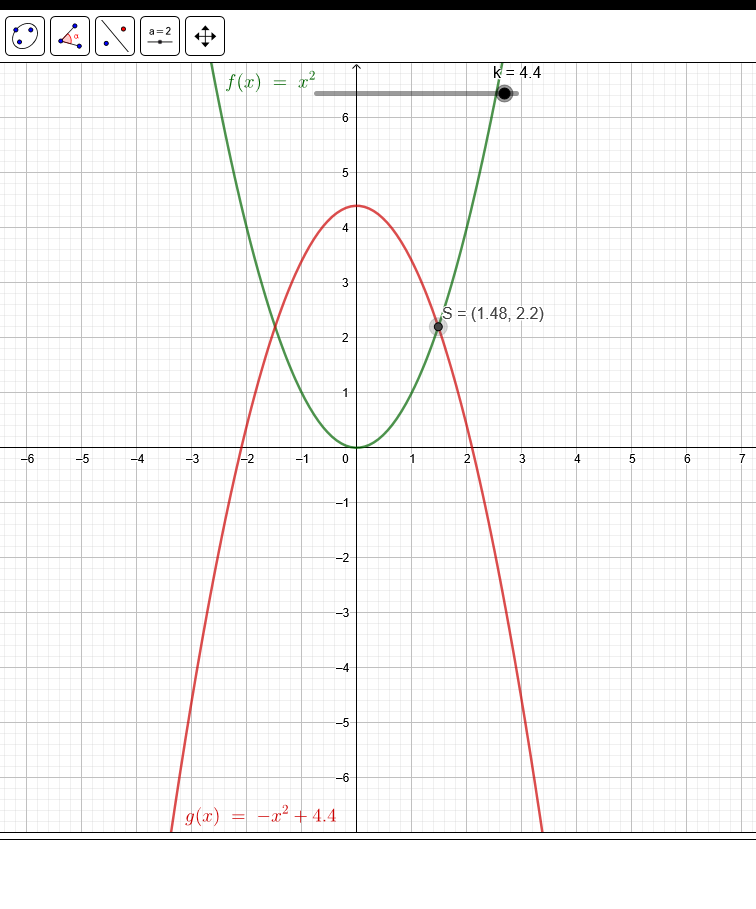

Text erkannt:

0