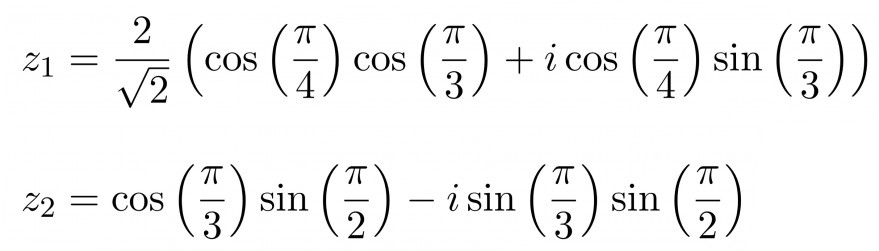
Text erkannt:
\( z_{1}=\frac{2}{\sqrt{2}}\left(\cos \left(\frac{\pi}{4}\right) \cos \left(\frac{\pi}{3}\right)+i \cos \left(\frac{\pi}{4}\right) \sin \left(\frac{\pi}{3}\right)\right) \)
\( z_{2}=\cos \left(\frac{\pi}{3}\right) \sin \left(\frac{\pi}{2}\right)-i \sin \left(\frac{\pi}{3}\right) \sin \left(\frac{\pi}{2}\right) \)
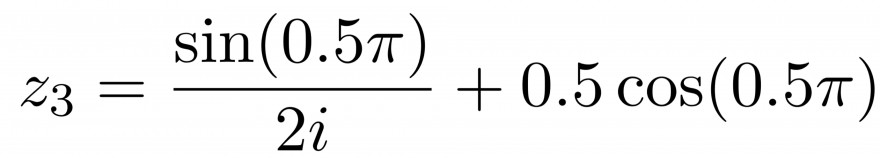
Text erkannt:
\( z_{3}=\frac{\sin (0.5 \pi)}{2 i}+0.5 \cos (0.5 \pi) \)
Wie berechne ich den Betrag und Winkel dieser Aufgaben? Hab da eine Tabelle für cos/sin pi usw...versteh es aber trotzdem nicht so :(
Wäre für professionelle Hilfe dankbar :)