Wie berechnet man die Nullstellen dieser Kurvenschar mit der abc-Formel?

Question

Aufgabe: f_a(x)= x² - ax - 3/4a²

Wir müssen die Nullstellen mit der abc-Formel berechnen und haben keine Ahnung wie das gehen soll.

Problem/Ansatz:

-Nullsetzen und dann abc Formel anwenden

-Welche Zahl ist a/b/c ???

Answer 1

a ist der Faktor vor x^2, b der vor x und c die Konstante. Um hier nicht durcheinander zu kommen soltest Du für Deine Funktion (oder auch für die Formel) Großbuchstaben verwenden:  \( f_A(x)= x^2 - Ax - 3/4A^2 \).

Answer 2

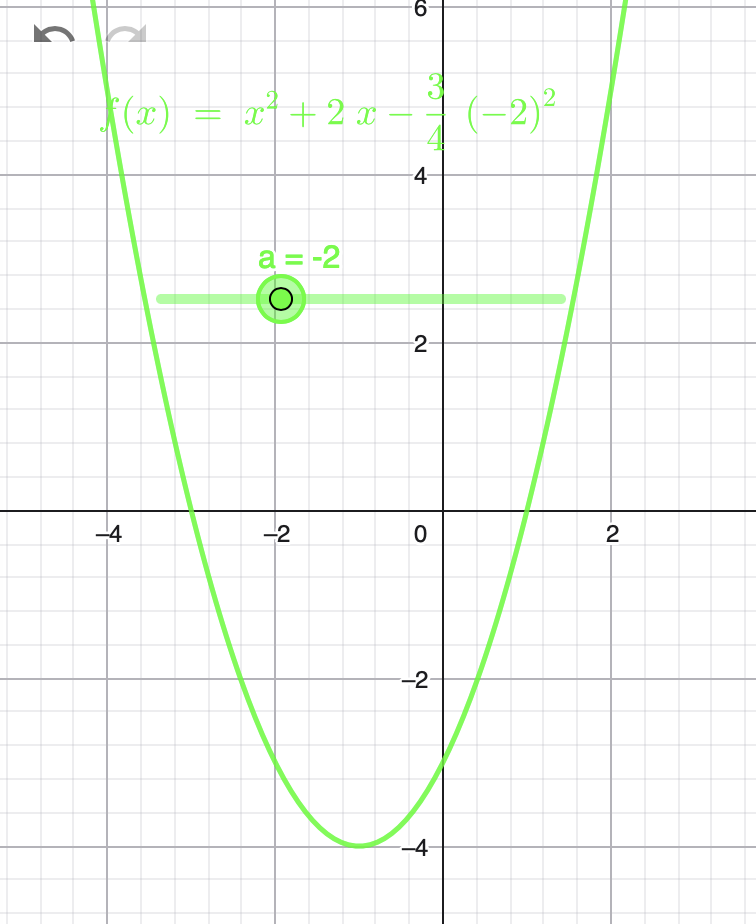
Wenn keine Lösungsform vorgegeben ist:

\( x^2-ax-\frac{3}{4}a^2=0 \)

\( x^2-ax=\frac{3}{4}a^2\)     quadratische Ergänzung: \( +(\frac{a}{2})^2 \)

\( x^2-ax+(\frac{a}{2})^2 =\frac{3}{4}a^2+(\frac{a}{2})^2  \)   2. Binom:

\( (x-\frac{a}{2})^2 =a^2|±\sqrt{~~~} \)

1.)

\( x-\frac{a}{2} =a\)

\( x_1=\frac{3}{2} a\)

2.)

\( x-\frac{a}{2} =-a\)

\( x_2=-\frac{a}{2} \)

Comments

Man beachte die Wörtlein:

Wir müssen die Nullstellen mit der abc-Formel berechnen ...

---

Du weißt doch, dass M. sich nie an die konkrete Vorgabe hält und seine Antworten immer (meist wesentlich aufwändigere) Alternativen darstellen. ;)

Answer 3

In f(x) = Ax² + Bx + C ist

A der Koeffizient vor dem x²
B der Koeffizient vor dem x
C der Konstante Summand

In deiner Funktion f(x) = 1x² - ax - 3/4·a² ist also

A = 1
B = -a
C = -3/4·a²

Daher sind die Nullstellen bei

x = (a ± √(a² - 4·1·(-3/4·a²)))/(2·1)
x = a/2 ± a

x = -1/2·a ; x = 3/2·a