Aufgabe:
Text erkannt:
M Q1 LK Vektorgeometrie auf dem Flughafen
Die Abbildung zeigt den gradlinigen Landeanflug der Lufthansa-Maschine auf den Flughafen Düsseldorf. Auf dem Rollfeld des Flughafens ist ein reges Treiben von fahrenden Follow-Me-Cars, den Lotsenfahrzeugen der Flugzeuge, zu beobachten. Vom Tower aus sehen Lotsen das unten abgebildete Follow-Me-Car, das sich
aktuell im Punkt \( F=(5|-4| 0) \) befindet und entlang des Vektors
(2) fortbewegt. In der gleichen Zeit,
die das Follow-Me-Car für seine Fahrt entlang des Vektors \( \vec{u} \) benötigt, bewegt sich das Flugzeug vom Punkt \( A=(1|4| 2) \) zum Punkt \( B=(2|2,5| 1,5) \)
Prüfen Sie, ob das Flugzeug gefahrlos landen kann. Gehen Sie so vor:
a) Stellen Sie für das Lotsenfahrzeug und für das Flugzeug je eine Geradengleichung auf.
b) Überprüfen Sie anhand des erarbeiteten Algorithmus, ob das Flugzeug gefahrlos landen kann.
c) Stellen Sie sich vor, dass das Lotsenfahrzeug und die Lufthansa-Maschine sich mit einer konstanten Geschwindigkeit fortbewegen. Überprüfen Sie mit dieser zusätzlichen Information erst graphisch und dann rechnerisch Ihre Lösung aus b).

Text erkannt:
Follow-Me-Car
a) \( g: \vec{x}=\left(\begin{array}{l}1 \\ 4 \\ 2\end{array}\right)+\left(\begin{array}{c}2-1 \\ 2,5-4 \\ 1,5-2\end{array}\right) \quad g: \vec{x}=\left(\begin{array}{c}s \\ -4 \\ 0\end{array}\right)+s \cdot\left(\begin{array}{c}0-5 \\ 2+4 \\ 0-0\end{array}\right) \)
\( =\left(\begin{array}{l}1 \\ 4 \\ 2\end{array}\right)+r \cdot\left(\begin{array}{ll}-1.5 \\ -0.5\end{array}\right) \quad=\left(\begin{array}{c}3 \\ -4 \\ 0\end{array}\right)+s \cdot\left(\begin{array}{c}-5 \\ 6 \\ 0\end{array}\right) \)
b) \( \left(\begin{array}{l}1 \\ 4 \\ 2\end{array}\right)+r \cdot\left(\begin{array}{c}1.5 \\ -1.5\end{array}\right)=\left(\begin{array}{c}5 \\ -4 \\ 0\end{array}\right)+s \cdot\left(\begin{array}{c}-5 \\ 6 \\ 0\end{array}\right) \quad\left(\begin{array}{l}1 \\ 4 \\ 2\end{array}\right)+c \cdot\left(\begin{array}{c}-1.5 \\ -0.5\end{array}\right)=\left(\begin{array}{c}5 \\ -4 \\ 0\end{array}\right)+s \cdot\left(\begin{array}{l}0 \\ 0\end{array}\right) \)
\( r-s_{s}=61.1,5 \quad r=6 \)
\( \begin{array}{rr}1.5 r-7.5 s=9 \\ -1.5 r+6 s=0 & -1.5 r+2 s=0 \\ -1.5 s=91:(-1,5) & -1,5.6+2 s=0 \\ s=-6 & -9+2 s=01+3 \\ 2 s & =91: 2 \\ s & =4.5\end{array} \)
\( -0.5 r=21 \cdot(-2) \)
\( -0, s r=2 \)
\( r=-4 \)
\Rightarrow> Das Flogzevg kann gefahrlas landen.
c)
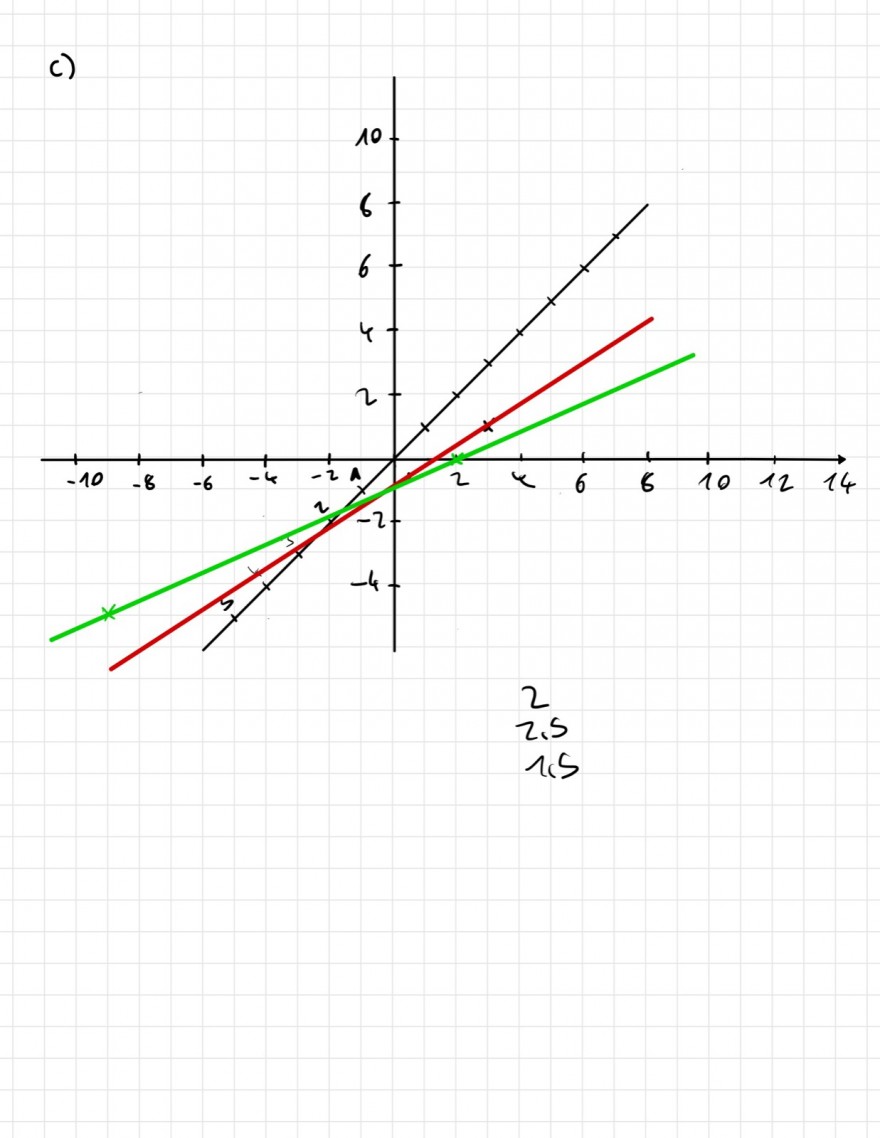
Problem/Ansatz:
… Habe ich die Aufgaben richtig bearbeitet ? Bei c) weiß ich auch nicht, was ich machen soll.