Question

Wie erstelle ich in Geogebra die Brenngerade d von einer Hyperbel?

Comments

Was ist eine Brenngerade?

---

In unserem Skript ist es folgendermaßen definiert:

Hyperbel
Betrachtet wird nun der Fall $\varepsilon>1$.
Definition 2.16 Eine Hyperbel ist die Menge aller Punkte $P$ im $\mathbb{R}^{2}$ deren Abstand zu einem festen Punkt $F$ identisch ist mit dem $\varepsilon$-fachen Abstand (mit $1<\varepsilon$ ) zu einer festen Geraden $d$. Die Hyperbel liegt in Standardform vor, wenn $F=(a \varepsilon, 0)$ für ein Zahl $a>0$ und $d=\{(x, y): x=a / \varepsilon\}$ sind.

---

Wie erstelle ich in Geogebra die Brenngerade d von einer Hyperbel?

Von welcher Hyperbel möchtest du denn die Brenngerade haben?

---

$h y p=\left\{(x, y) \in \mathbb{R}^{2}: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\right\} .$

---

Dann zeichne doch mal die Hyperpel in Geogebra ein. Mal schauen, ob du das hin bekommst.

---

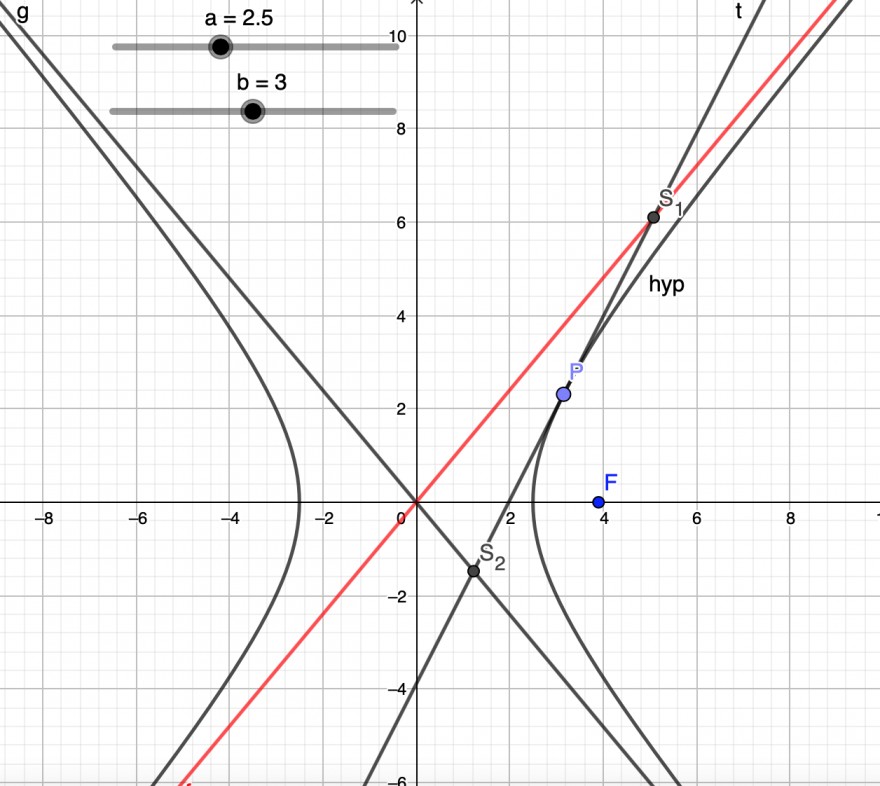
Das habe ich bereits geschafft. Vielleicht um die Aufgabenstellung nochmal etwas deutlicher zu machen:

a) Erstellen Sie zwei Schieberegler $a$ und $b$ für eine Zahl jeweils in einem sinnvollen Intervall
mit $b \geq a>0$
b) Erstellen Sie die Hyperbel hyp $=\left\{(x, y) \in \mathbb{R}^{2}: \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1\right\}$.
c) Konstruieren Sie den Brennpunkt $F$, die Brenngerade d und die Asymptoten der Hyperbel.
Färben Sie den Brennpunkt sowie die Brenngerade blau und die Asymptoten rot ein.
d) Erzeugen Sie die Tangente $t$ an dem Berührpunkt $P$, welcher auf der Hyperbel liegt.
e) Konstruieren Sie die Schnittpunkte $S_{1}$ und $S_{2}$ der Tangente mit den Asymptoten.

Das ist unsere Aufgabe, Teilaufgabe a) und b) habe ich hinbekommen, auch den Brennpunkt F und die Asymptoten habe ich konstruiert. Nur bei der Brenngerade scheitert es..

Answer 1

Schau mal unter Wikipedia

https://de.wikipedia.org/wiki/Hyperbel_(Mathematik)#Leitlinien-Eigen…

Die Brenngerade ist nur ein anderer Ausdruck für Leitlinie.

Dort steht auch die Gleichung der Leitlinie als x = ± a²/e

Das sieht also in Geogebra so aus