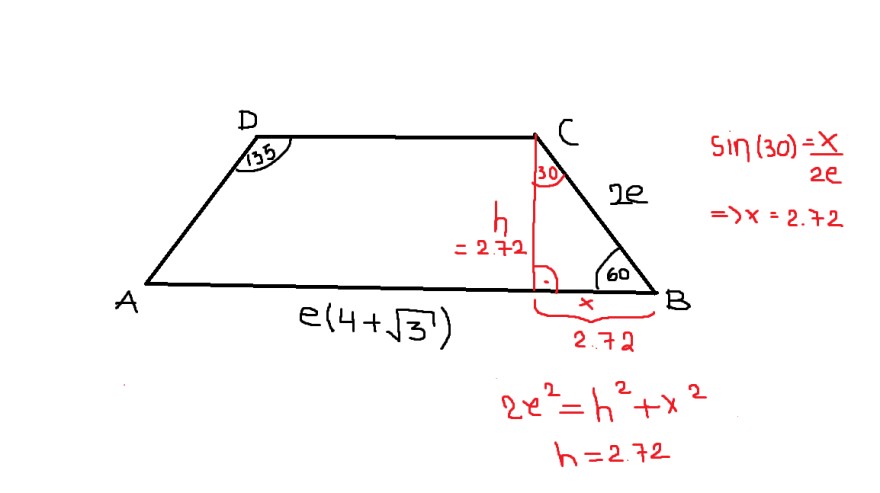
ich habe ein Trapez mit den *Schwarz* eingetragenen Angaben gegeben
(AD und BC sind ungleich)
ich muss zeigen, dass A= \( \frac{e^2}{2} \) * ( 7\( \sqrt{3} \)+3 ) gilt
also, erstmal gilt A= (a+b)/2*h
mit Rot habe ich meine Gedanken eingetragen.
also ich habe erstmal h eingezeichnet
dann habe ich den Winkel ergänzt, indem ich 180-90-60 gerechnet habe (=30)
dann habe ich versucht, über sin(30) die untere, kleine Seite rauszubekommen und habe 2.72 raus.
2e2= 2.722+h2
h2 ist also7.39
h ist also 2.72
irgendwie passt das aber nicht zu der gegebenen Formel
kann mir jemand bitte erklären, wie man auf die Formel kommt?
geht vermutlich einfacher, als was ich hier versucht habe, kam aber nur auf diese Idee...