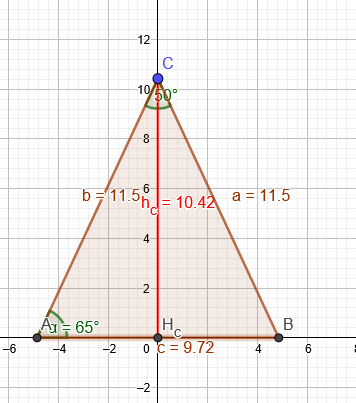
"Von einem gleichschenkeligen Dreieck \( (a=b) \) kennt man die folgenden Bestimmungsstücke. Berechne die fehlenden Seitenlängen und Winkel des Dreiecks! \( a=11,5, \alpha=65^{\circ} \)"
sin(65°)=\( \frac{h_c}{11,5} \)
cos(65°)=\( \frac{c}{2*11,5} \)
γ=180°- 2*65°