Aufgabe:
Die Dachfläche wird als Aussichtsplattform genutzt. Dorthin gelangt man über eine Treppe, die an der Kante B2C2 endet. Für den Sicherheitsaspekt ist die Steilheit der Treppe interessant. Dazu wird die Ebene E betrachtet, die die Lage (Neigung) dieser Treppe beschreibt. In dieser Ebene E liegt der Punkt P (170/120/0). Stellen Sie eine Gleichung dieser Ebene in Parameterdarstellung auf. Berechnen Sie einen Vektor, der orthogonal zu dieser Ebene verläuft.
Problem/Ansatz:
Ich stehe gerade absolut auf dem Schlauch und komme überhaupt nicht weiter. Hat jemand hierzu einen Rechenweg mit Lösung? Der Rechenweg wäre sehr hilfreich, um die Lösung auch zu verstehen, wenn ich es nachrechne. Vielen Dank im voraus! 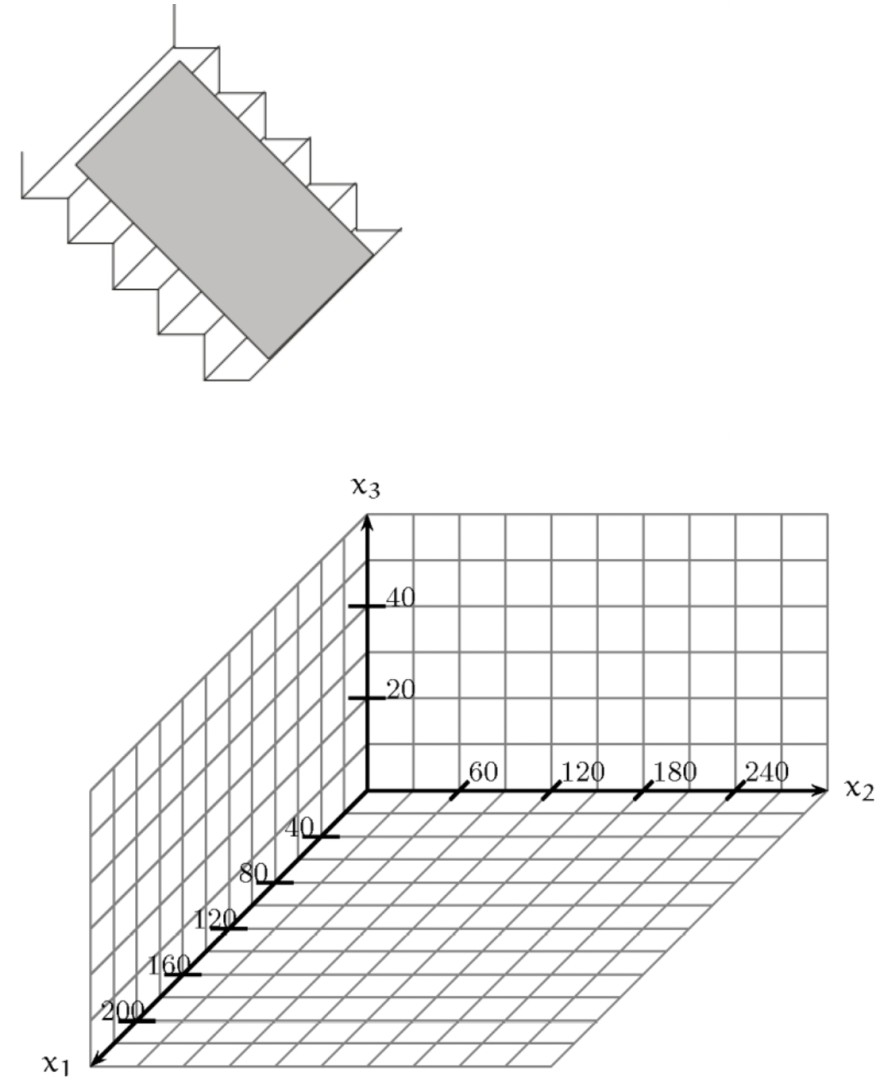
Text erkannt:
\( x_{3} \)