Räumliche Geometrie - Brennpunkte?

Question

Hallo zusammen! Hätte jemand eventuell eine Idee zu dieser Aufgabe? Ich komme da einfach auf keinen Lösungsweg.

Vorgelegt seien zwei Brennpunkte \( F_{1} \) und \( F_{2} \) einer Hyperbel, eine Halbgerade \( \left[A B\right. \) mit \( |A B|<\left|F_{1} F_{2}\right| \) und ein Punkt \( C \in[A B \) mit \( |C A|=\left|F_{1} F_{2}\right| \). Die Hyperbel bestehe aus den Punkten \( P \), die \( \left|P F_{1}\right|-\left|P F_{2}\right|=|A B| \) erfüllen. Konstruieren Sie:

a Zwei Punkte der Hyperbel, die nicht in der Strecke \( \overline{F_{1} F_{2}} \) enthalten sind.
b Einen Punkt der Hyperbel, der in der Strecke \( \overline{F_{1} F_{2}} \) enthalten ist.

Vielen Dank schon mal!

Answer 1

Hallo,

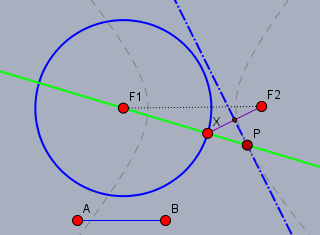
Zeichne einen Kreis mit Radius \(|AB|\) um einen der Brennpunkte (z.B. \(F_1\)). Wähle einen beliebigen Punkt \(X\) auf dem Kreis. Die Mittelsenkrechte (blau Strich-Punkt) der Strecke \(XF_2\) schneidet die Gerade (grün) durch \(F_1X\) in \(P\).

Da \(|PX| = |PF_2|\) ist \(|PF_1| - |PF_2| = |AB|\).

zu (b): liegt \(X\) auf der Strecke \(F_1F_2\), so liegt auch \(P\) auf dieser Strecke.

Hinweis: die Mittelsenkrechte ist auch gleichzeitig die Tangente an die Hyperbel in \(P\).

Hinweis 2: die im Wiki-Artikel beschriebene Einschränkung, dass der (Leit-)Kreis um \(F_1\) nur den rechten Ast der Hyperbel erzeugt, ist falsch. Eine ganze Umdrehung von \(X\) erzeugt beide Äste.

Gruß Werner

Comments

.. weil ich gerade frei habe:

Tipp: schiebe doch mal den Punkt \(F_2\) in den Kreis hinein ;-)