Hallo,
... da laut Aufgabenstellung der Mittelpunkt der Halbkreise nicht gegeben ist.
das kann so nicht sein. Der linke grüne Kreisbogen geht durch die Punkte \(A\) und \(E\). Und wenn der Punkt \(B\) nicht sein Mittelpunkt wäre, dann wäre er völlig unnütz. Abgesehen davon wäre die Aufgabe nicht ausreichend beschrieben.
Genauso muss \(A\) der Mittelpunkt des rechten Kreisbogens sein. Alles ander macht keinen Sinn. Und so lässt sich dann auch eine Lösung finden. Das Wissen, dass die drei Winkel in einem Dreieck 180° ergeben, reicht dazu aus.
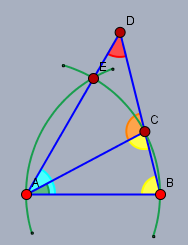
Das Dreieck \(\triangle ABC\) ist gleichschenklig, daher ist \(\angle ACB = \angle CBA = \beta\) (gelb). Also ist$$2 \beta + \alpha = 180° \implies \beta = 90° - \frac{\alpha}{2}$$und der orange Winkel \(\angle DCA = \gamma\) ist Nebenwinkel zu \(\beta\)$$\gamma = 180° - \beta = 90° + \frac{\alpha}{2}$$Der hellblaue Winkel muss \(60°\) betragen, da \(\triangle ABE\) ein gleichseitiges Dreieck ist. Und die Winkelsumme im Dreieck \(\triangle ACD\) ist$$\begin{aligned}60° - \alpha + \gamma + \delta &= 180°\\\delta &= 180° - 60° + \alpha - \gamma\\ &= 120° + \alpha -90° - \frac{\alpha}{2}\\ &= 30° + \frac{\alpha}{2} = 44°\end{aligned}$$Eine alternative Lösung sähe so aus. Zeichen dazu zwei zu \(AB\) orthogonale Geraden durch die Punke \(B\) und \(D\). Sowie eine zu \(AD\) orthogonale Gerade durch \(A\). Letztere ist die Symmetrieachse zu \(\triangle ABC\) die \(BD\) in \(M\) schneidet.
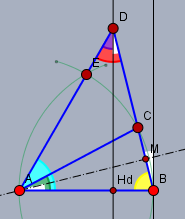
Das Dreieck \(\triangle ABM\) ist rechtwinklig und der Winkel \(BAM\) (weiß) ist \(\alpha/2\). Folglich muss der weiße Winkel bei \(B\) ebenso \(=\alpha/2\) sein und auch der Winkel \(\angle H_dDB\) (weiß) (Wechselwinkel an Parallelen). Das Dreieck \(\triangle AH_dD\) ist auch rechtwinklig. Daraus folgt, \(\angle ADH_d = 30°\) (lila) und $$\delta = 30° + \frac{\alpha}{2}$$Gruß Werner