Mehrere normalverteilte Zufallsvariablen, Wahrscheinlichkeitstheorie

Question

Aufgabe:

X1 und X2 seien unabhängige Zufallsvariablen, beide sind normalverteilt mit Erwartungswert 6 und Varianz 8. Betrachten Sie für die folgenden Aufgaben die Zufallvariable M = 0.5(X1+X2)

a) Was können Sie über die Verteilung von M Aussagen?

b) Wie groß ist die Wahrscheinlichkeit, dass 2<= M < 10 gilt?

c) Wie groß ist die Wahrscheinlichkeit, dass M < 0 gilt?

d) Wie groß ist c, wenn P(M>c) = 0.95 gilt?

e) Wie groß ist c, wenn P(6-c < M < 6+c) = 0.95 gilt?

Problem/Ansatz:

Ich habe leider garkeinen richtigen Ansatz, wie ich an so eine Aufgabe herangehen soll. Ich finde auch keine passenden Videos zu dem Thema. Im Bild hab ich meine Idee zur a), glaube aber nicht, dass es so richtig ist. Ab Aufgabe B weiß ich garnicht mehr, wie ich das machen kann. Ich weiß auch nicht wie ich mit der 0.5 umgehen soll, sonst hab ich immer nur aufgaben zu X1+X2 oder X1-X2 gesehen.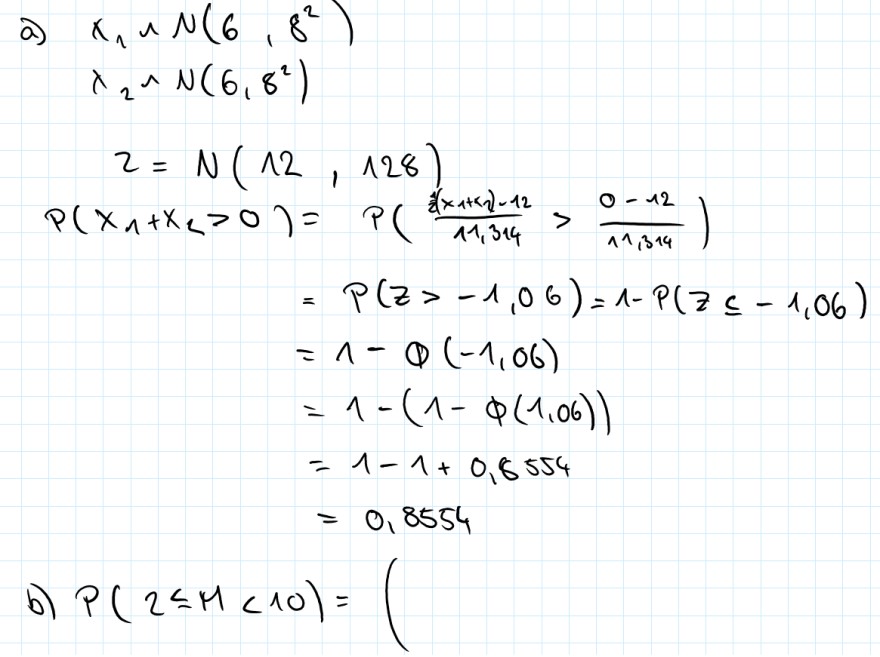

Text erkannt:

a) \( x_{1} \backsim N\left(6,8^{2}\right) \)
\( \lambda_{2} \wedge N\left(6,8^{2}\right) \)
\( z=N(12,128) \)
\( P\left(x_{1}+x_{2}>0\right)=P\left(\frac{z^{2}\left(x_{1}+12\right)-12}{11,314}>\frac{0-12}{11,314}\right) \)
\( =P(z>-1,06)=1-P(z \subseteq-1,06) \)
\( =1-\Phi(-1,06) \)
\( =1-(1-\phi(1,06)) \)
\( =1-1+0,8554 \)
\( =0,8554 \)
b) \( P(2 \leqslant M<10)= \)

Answer 1

Aloha :)

\(X_1\) und \(X_2\) sind normalverteilt mit \(\mu_1=\mu_2=6\) und \(\sigma_1^2=\sigma_2^2=8\).

zu a) Die Summe zweier normalverteilter Zufallsgrößen ist wieder normalverteilt, wobei sich die Erwartungswerte und die Varianzen addieren. Daher gilt für \(M=\frac12\left(X_1+X_2\right)\):$$\mu=\left<\frac12\left(X_1+X_2\right)\right>=\frac12\left<X_1+X_2\right>=\frac12\left(\mu_1+\mu_2\right)=6$$$$\sigma^2=\operatorname{Var}\left(\frac12\left(X_1+X_2\right)\right)=\left(\frac12\right)^2\operatorname{Var}(X_1+X_2)=\frac14\left(\sigma_1^2+\sigma_2^2\right)=4\implies\sigma=2$$

zu b) Hier ist genau das \(2\sigma\)-Intervall gefragt, also \((\mu-2\sigma\le M<\mu+2\sigma)\).

Die Wahrscheinlichkeit dafür sollte man auswendig kennen: \(p_b\approx95,45\%\)

zu c) Hier müssen wir normalisieren:$$p_c=P(M<0)=\phi\left(\frac{0-6}{2}\right)=\phi(-3)=1-\phi(3)\approx0,1350\,\%$$

zu d) Die Rechnung ist etwas aufwändiger:$$0,95=P(M>c)=1-P(M<c)\implies P(M<c)=0,05\implies$$$$\phi\left(\frac{c-6}{2}\right)=0,05\implies\frac{c-6}{2}=\phi^{-1}(0,05)\approx-1,644854\implies c\approx2,7103$$

zu e) Jetzt will der Aufgabensteller es aber wissen:$$0,95=P(6-c<M<6+c)=P(M<6+c)-P(M<6-c)$$$$\phantom{0,95}=\phi\left(\frac{(6+c)-6}{2}\right)-\phi\left(\frac{(6-c)-6}{2}\right)=\phi\left(\frac c2\right)-\phi\left(-\frac c2\right)$$$$\phantom{0,95}=\phi\left(\frac c2\right)-\left(1-\phi\left(\frac c2\right)\right)=2\phi\left(\frac c2\right)-1\quad\implies$$$$2\phi\left(\frac c2\right)=1,95\implies\phi\left(\frac c2\right)=\frac{1,95}{2}\implies\frac c2=\phi^{-1}(0,975)\approx1,96\implies c\approx3,92$$