Bestimmen Sie den maximalen Definitionsbereich der Funktion f mit f(x)=√{x2-x-12} .

Question

Aufgabe:

Bestimmen Sie den maximalen Definitionsbereich der Funktion $f$ mit $f(x)=\sqrt{x^{2}-x-12}$.
Hinweis: $\infty$ können Sie mit "inf" und $-\infty$ mit "-inf" darstellen.
$\mathbb{D}=$\begin{tabular}{|l|l|l|l|l|l|l|l|l|}
\hline ( oder [ & \\
\hline
\end{tabular}

Problem/Ansatz:

Was kommt hier als Lösung raus komme einfach nicht drauf und bin am verzweifeln leute .. Danke im Voraus. Gerne mit Lösungsweg :***

Answer 1

Du musst schauen wo $x^2 - x -12 \ge 0$ gilt.

Answer 2

x²-x-12 >=0

(x-4)(x+3) >=0

Fallunterscheidung:

1. x>=4 u. x >=-3 

x>=4

2. x<=4 u. x<= -3 

x <= -3

D = R \ (-3; 4)

Answer 3

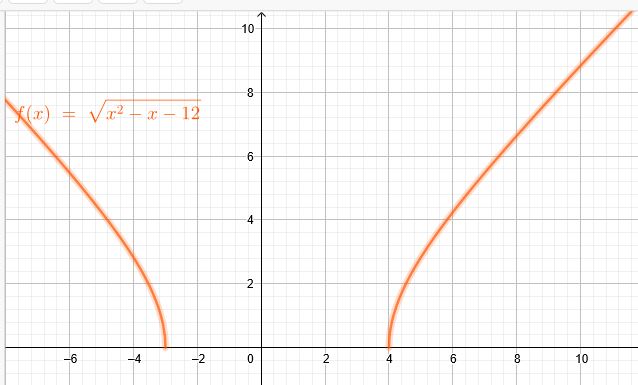
$f(x)=\sqrt{x^{2}-x-12}$

$x^2-x-12=0$

$x^2-1*x=12$

$(x-0,5)^2=12+0,5^2=12,25|\sqrt{~~}$

1.)$x-0,5=3,5$

$x₁=4$

2.) $x-0,5=-3,5$

$x₂=-3$

$f(x)=\sqrt{(x-4)*(x+3)}$

Der Term unter der Wurzel darf nicht kleiner als 0 werden.

Wann wird er kleiner als 0?