Grenzproduktivität von x(r) = 5*r^{2/3} - 20 berechnen

Question

Ich komme bei der Aufgabe nicht mehr weiter. ?

Ein Unternehmen kann ein Produkt entsprechend der Produktionsfunktion herstellen, wobei x(r) die hergestellte Menge und r die Einsatzmenge eines Prokduktionsfaktors ist. Berechnen Sie die Grenzproduktivität. Nimmt die Grenzproduktivität mit steigendem Faktoreinsatz zu oder ab?

x(r)= 5* ³√r² -20  

x(r)= 5*r^2/3 - 20

x'(r)= 2/3 *5r ^2/3-1

x'(r)= 10/3r ^-1/3                         x'(r)= 0

 

10/3r ^-1/3= 0

 

Answer 1

Ich bin nicht ganz sicher, was das da bedeuten soll. Ist das schon der Versuch einer Rechnung?

 

Wenn ja, dann sind da einige Fehler drin.

Also erstmal solltest du dir über die Definition der Grenzproduktivität im Klaren sein:
Man versteht darunter die Änderung der Produktivität bei einer kleinen Änderung der Einsatzmenge, mit anderen Worten also die partielle Ableitung der Produktivität nach der Einsatzmenge.

Wenn also die Produktionsfunktion

x(r) = 5*^³√(x²) - 20

ist, dann kann man die Funktion gerne erstmal in eine einfachere Form bringen, aber richtig! :-)
x(r) = 5*x^2/3 - 20

Das reicht schon völlig aus, jetzt kann man die Ableitung bilden:
x'(r) = 10/3*x^-1/3

Ach, jetzt verstehe ich erst, was du da gerechnet hast. Du solltest aber darauf achten, dass du Funktion und Ableitung nicht verwechselst: die Ableitung bekommt den Strich, also x' ist die Ableitung von x.

Nun sollst du aber nicht die Nullstellen der Ableitung suchen (das würdest du für eine Extremwertaufgabe machen) sondern einfach nur ihren globalen Verlauf diskutieren.

 

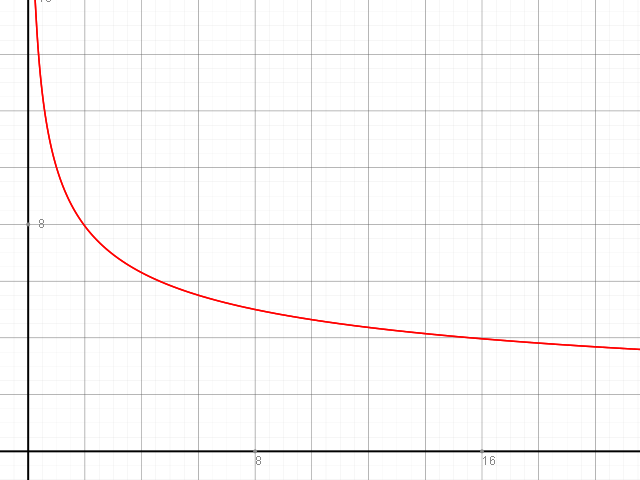
Wie man sieht fällt die Grenzproduktivität also für wachsenden Faktoreinsatz.
Beachte, dass das nicht bedeutet, dass die Produktivität niedriger wird: es bedeutet nur, dass sie immer langsamer wächst.