Was du gerechnet hast hat soweit Hand und Fuß, nur im letzten Schritt hast du einen Fehler gemacht: Wenn du aus
-1/2 x3 + x
ein x ausklammerst, dann darfst du die 1 nicht vergessen!
-1/2 x3 + x = x*(-1/2 x² + 1)
Damit bekommst du die eine Lösung x = 0, die du bereits genannt hast aber noch zwei weitere, die sich aus den Nullstellen des zweiten Faktors ergeben
0 = -1/2 x² + 1
x² = 2
x = ±√2
Wegen der Symmetrie der Funktion reicht es nun den Höhenunterschied für eine Funktion auszurechnen, also zu zeigen, dass
|f(0) - f(√2)| = 0.5
gilt. Das ist sehr leicht auszurechnen und du wolltest ja nur Ansätze haben... :-)
b) Hier brauche ich nun das Schaubild der Funktion, deswegen reiche ich es gleich mal nach, gemeinsam mit dem gewünschten Trapez:
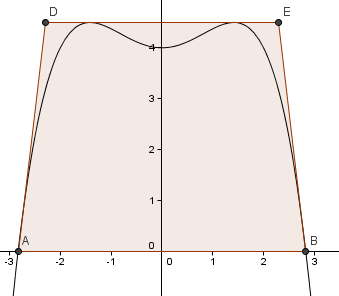
Das braune ist die Kunststoffplatte, aus der der Zahn ausgeschnitten werden soll.
Die Grundseite kennen wir bereits:
AB = 4*√2
Außerdem wissen wir die y-Koordinate der Punkte D und E:
y = f(√2) = 4.5
Jetzt brauchen wir noch die Funktion der Tangenten im Punkt A, dann können wir die x-Koordinate von D ausrechnen und kennen dann die Höhe h und die Länge der beiden parallelen Seiten a und c des Trapezes und können gemäß
A = h*(a+c)/2
den Flächeinhalt ausrechnen.
Die Tangente besitzt zwei charakteristische Größen:
I. t(-2√2) = 0
II. t'(-2√2) = f'(-2√2)
Da sie eine lineare Funktion ist, können wir sie also in der Form
t(x) = m*(x+2√2)
schreiben, wobei m = f'(-2√2) gilt.
f'(x) = -1/2 x3 + x
f'(-2√2) = 1/2*16*√2 -2√2 = 6√2
Die Tangente lautet also: t(x) = 6√2*(x+2√2)
Um die x-Koordinate xD von D zu ermitteln, muss t(xD) = 9/2 gesetzt werden:
9/2 = 6√2*(xD+2√2)
3/(4√2) = xD + 2√2
xD = -2√2 + 3/(4√2) ≈ -2.2981
Damit erhält man c = 2*|xD| = |3/(2√2) - 4√2| ≈ 4.5962
Wir haben jetzt also c und außerdem
a = 4√2
h = 9/2
Damit folgt:
A = 9/2*(4√2 + |3/(2√2) - 4√2|)/2
A ≈ 23.07 m²
Um den Materialverlust auszurechnen musst du nun die Fläche AZ des Zahns ausrechnen, indem du die Funktion f(x) zwischen ihren beiden Nullstellen integrierst.
Az = ∫ab f(x) dx
a = -2√2
b = 2√2
Den prozentualen Verlust erhält man dann gemäß:
p = (A-Az)/A
c) Hier soll das maximale Rechteck der folgenden Form gefunden werden:

Das wird am besten abhängig von der x-Komponente des Punktes B berechnet:
Das Rechteck hat dann den Flächeninhalt:
AR(x) = 2x*f(x)
AR(x) = -1/4 x5 + x3 + 8x
Für einen Extremwert wird AR'(x) = 0 gesetzt und die möglichen Lösungen berechnet.
Man erhält die Lösung x = 2, für die Breite also x = 4. (Rechne das nach!)
d) Für einen flüssigen Übergang ohne Knick müssen im Übergangspunkt nicht nur die Funktionswerte, sondern auch die Ableitungen übereinstimmen. Allerdings ist f(x) nach dem Übergangspunkt eine steigende Funktion und die Unterseite (ich nenne sie mal h(x) eine fallende Funktion. Daraus folgt, dass ein flüssiger Übergang nur für eine senkrechte Tangente, also eine unendlich große Steigung möglich ist.
Ganzrationale Funktionen sind aber auf ganz ℝ differenzierbar, insbesondere ist ihre Steigung auf einem abgeschlossenen Intervall also beschränkt. Daraus folgt, dass eine ganzrationale Funktion keinen solchen Punkt mit unendlich hoher Steigung geben kann, also ist immer ein Knick im Übergang.