Berechnen Sie die Dimensionen von \operatorname{Ann}(U) und \operatorname{Null}(X) .

Question

Definiere die Vektoren $v_{1}, v_{2} \in V_{4}(K)$ und $z_{1}, z_{2}, z_{3}, z_{4} \in Z_{4}(K)$ durch

Gegeben seien die Untervektorräume $U:=L\left(\left\{v_{1}, v_{2}\right\}\right)$ von $V_{4}(K)$ und $X:=L\left(\left\{z_{1}, z_{2}, z_{3}, z_{4}\right\}\right)$ $\operatorname{von} Z_{4}(K)=\left(V_{4}(K)\right)^{*}$.
(a) Berechnen Sie die Dimensionen von $\operatorname{Ann}(U)$ und $\operatorname{Null}(X)$. Hinweis: Satz 8.10.

Satz 8.10

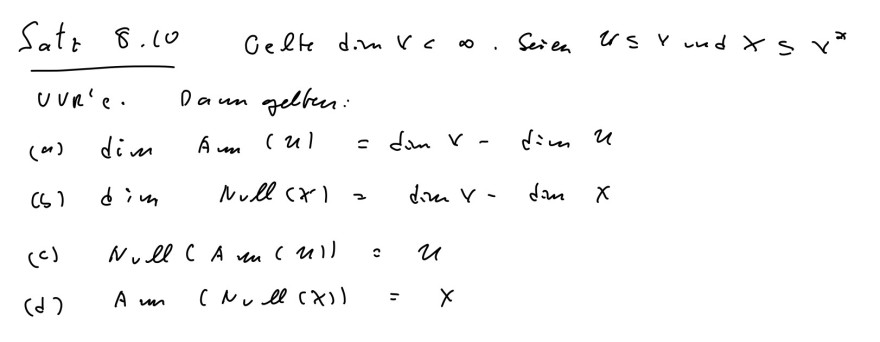
kann mir wer bitte zeigen wie ich die Dimension ausrechne. LG

Comments

Du musst uns schon mitteilen,
was $v_1$ und $v_2$ sind, ebenso
$z_1,z_2,z_3,z_4$.

---

Sorry scheint wohl untergegangen zu sein