Aloha :)
zu a) Die Punkte aus der Menge \(D\coloneqq\{(x;y)\in\mathbb R^2\,\big|\,\green{x^2+y^2\le1}\;\land\;\red{x+y\ge0}\}\) liegen
\(\green{\text{innerhalb eines Kreises mit Radius \(1\) um den Urpsrung}}\) und
\(\red{\text{oberhalb oder auf der Geraden \(y=-x\)}}\)
Unser guter Freund Wolfram zeichnet das so:
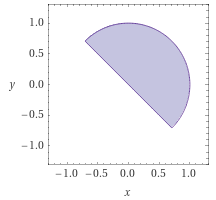
zu b) Die Integrationsgrenzen in kartesischen Koordinaten \((x;y)\) sowie die Bestimmung des Integrals selbst sind in kartesischen Koordinaten recht fummelig. Daher empfehle ich den Übergang zu Polarkoordinaten:$$\binom{x}{y}=\binom{r\cos\varphi}{r\sin\varphi}\quad;\quad r\in[0|\infty)\;;\;\varphi\in[0;2\pi]\quad;\quad dx\,dy=r\,dr\,d\varphi$$
Die grüne Bedingung schränkt das Integrationsintervall für den Radius ein:$$\green{x^2+y^2\le1}\implies(r\cos\varphi)^2+(r\sin\varphi)^2\le1\implies r^2\le1\stackrel{(r\ge0)}{\implies}\green{r\in[0;1]}$$
Die rote Bedingung schränkt das Integrationsintervall für den Polarwinkel ein. Man erkennt direkt aus der Abbildung, dass \(\red{\varphi\in[-\frac\pi4\,\big|\,\frac{3\pi}{4}]}\) gelten muss. Ich denke, es reicht auch, wenn du dieses Intervall mit der Zeichnung begründest, sonst hättest du es ja nicht zu zeichnen brauchen. Wenn du das trotzdem rechnerisch zeigen möchtest, kannst du dir Folgendes überlegen:$$\red{x+y}=r\cos\varphi+r\sin\varphi=r\cdot\overbrace{\sqrt2\,\underbrace{\frac{1}{\sqrt2}}_{=\sin\frac\pi4}}^{=1}\cos\varphi+r\cdot\overbrace{\sqrt2\,\underbrace{\frac{1}{\sqrt2}}_{=\cos\frac\pi4}}^{=1}\sin\varphi$$$$\phantom{x+y}=\sqrt2\,r\left(\sin\frac\pi4\cos\varphi+\cos\frac\pi4\sin\varphi\right)=\red{\sqrt2\,r\sin\left(\varphi+\frac\pi4\right)}\red{\ge0}$$Damit die Sinus-Funktion \(\ge0\) ist, muss \(\red{\varphi\in[-\frac\pi4\,\big|\,\frac{3\pi}{4}]}\) gelten.
Damit können wir nun das gesuchte Integral formulieren:$$I=\int\limits_D(x+y)^2\,dx\,dy=\int\limits_{r=0}^1\;\;\int\limits_{\varphi=-\frac\pi4}^{\frac{3\pi}{4}}(r\cos\varphi+r\sin\varphi)^2\,r\,dr\,d\varphi$$$$\phantom I=\int\limits_{r=0}^1r^3\,dr\int\limits_{\varphi=-\frac\pi4}^{\frac{3\pi}{4}}(\underbrace{\cos^2\varphi+\sin^2\varphi}_{=1}+2\sin\varphi\cos\varphi)\,d\varphi=\left[\frac{r^4}{4}\right]_{0}^1\cdot\left[\varphi+\sin^2\varphi\right]_{-\frac\pi4}^{\frac{3\pi}{4}}$$$$\phantom I=\frac14\cdot\left[\left(\frac{3\pi}{4}+\frac12\right)-\left(-\frac\pi4+\frac12\right)\right]=\frac\pi4$$