Bew Eigenvektor Matrix durch Induktion

Question

Sei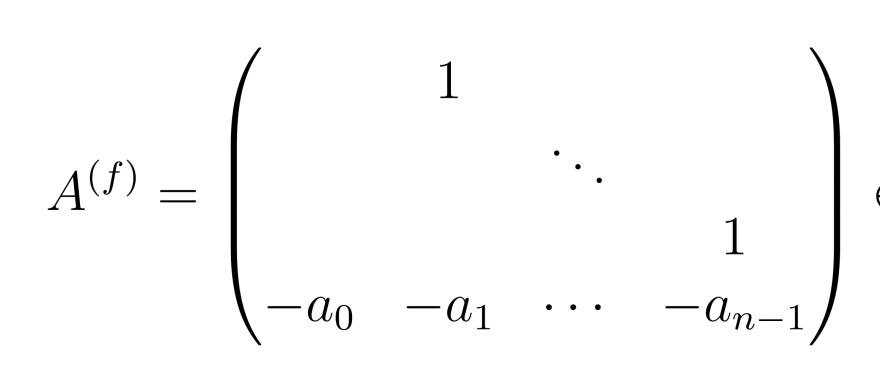

$v_{0}:=\left(1, \lambda, \lambda^{2}, \ldots, \lambda^{n-1}\right)^{t r} \in M(n \times 1, K)$

Sei $\lambda \in K$ eine doppelte Nullstelle von $f$. Zeigen Sie, dass
$v_{1}:=\left(0,1,2 \lambda, \ldots,(n-1) \lambda^{n-2}\right)^{t r} \in M(n \times 1, K)$
die Gleichung
$A^{(f)} \cdot v_{1}=\lambda \cdot v_{1}+v_{0}$
erfüllt.

Ich würde das Ganze mit Induktion beweisen. Allerdings komme ich beim Induktionsspule Anfang auf 2Lamda=-a1

Comments

Allerdings komme ich beim Induktionsspule Anfang

So ist das halt, wenn man die Autokorrektur nicht überwacht.
Ich würde zur Abhilfe einen Kondensator vorschalten.

---

Ja mein Fehler….

---

Sei $\lambda \in K$ eine doppelte Nullstelle von $f$.

Falls es so gemeint ist: Das charakteristische Polynom von $A^{(f)}$ lautet bekanntlich
$p_A(x)=x^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$.
Wenn $\lambda\in K$ eine doppelter Eigenwert von $A^{(f)}$ ist, dann ist $p_A(\lambda)=p_A^\prime(\lambda)=0$.
Damit ließe sich die Aussage direkt beweisen.