Wie stellt man diese Gleichung auf?

Question

Aufgabe:Stelle die Gleichung der Tangente von f an der Stelle π auf.

Problem/Ansatz:

Kann mir bitte jemand erklären wie das geht?

Text erkannt:

2. Stelle die Gleichung der
a) $f(x)=2 \sin (x)$
b) $f(x)=3 \sin (3 x)$

Answer 1

t(x) = (x-pi)*f '(pi) + f(pi)

a) f '(x) = 2*cos(x)

b) f '(x) = 9*cos(3x)

sin(pi)= 0

sin(3*pi) = 0

cos(pi) = -1

cos (3pi)= -1

Comments

b) f '(x) = -9*cos(3x)

Warum das?

---

Das Minus ist mir reingerutscht.

Ich habe es ediert. Danke.

Answer 2

Die Tangente an der Stelle pi lautet immer

t(x) = f'(pi) * (x - pi) + f(pi)

Setze jetzt ein und vereinfache den Ausdruck soweit du kannst.

a) t(x) = 2·(pi - x)

b) t(x) = 9·(pi - x)

Answer 3

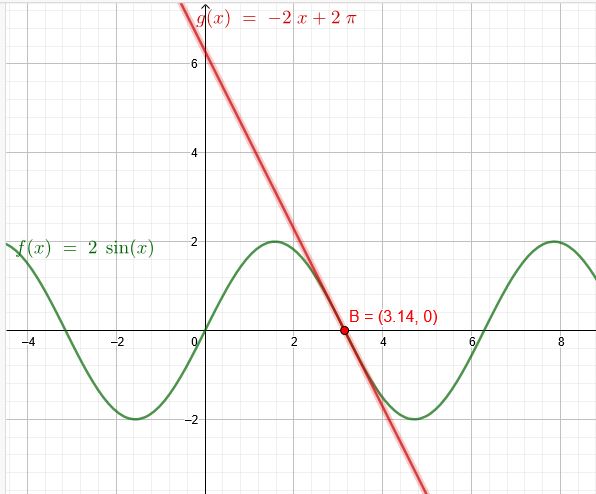
a)

$f(x)=2 \sin (x)$

Stelle die Gleichung der Tangente von f an der Stelle $π$ auf.

$f(π)=2 \sin (π)=0$

$f´(x)=2 \cos (x)$   

$f´(π)=2 \cos (π)=-2$ 

Allgemeine Punktsteigungsformel einer Geraden:

$\frac{y-y_1}{x-x_1}=m$

$\frac{y-0}{x-π}=-2$  

$y=-2x+2*π$