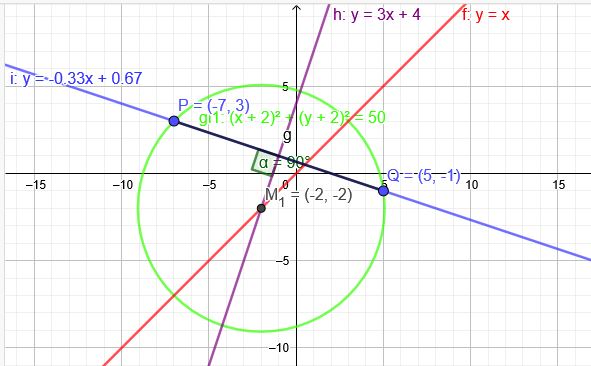
Mittelpunkt auf \(y=x\)
Geradengleichung durch \(P(-7|3) \) \(Q(5|-1)\)
\(y=-\frac{1}{3}x+\frac{2}{3}\)
Mittelsenkrechte der Strecke PQ schneidet \(y=x\) in \(M(-2|-2)\)
Kreisgleichung:
\((x+2)^2+(y+2)^2=r^2\)
\(P(-7|3) \) liegt auf diesem Kreis:
\((-7+2)^2+(3+2)^2=r^2\) → \(r^2=50\)
\((x+2)^2+(y+2)^2=50\)
Punktprobe für \(Q(5|-1)\)
\((5+2)^2+(-1+2)^2=50\)→ \(49+1=50\) ✓