Durch C0-Raum gegebene Funktionen auf Stetigkeit überprüfen

Question

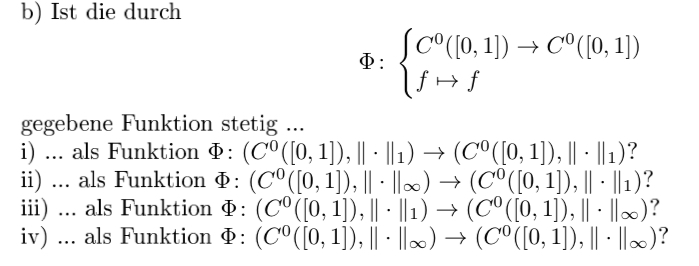
Text erkannt:

b) Ist die durch
\( \Phi:\left\{\begin{array}{l} C^{0}([0,1]) \rightarrow C^{0}([0,1]) \\ f \mapsto f \end{array}\right. \)
gegebene Funktion stetig ...
i) ... als Funktion \( \Phi:\left(C^{0}([0,1]),\|\cdot\|_{1}\right) \rightarrow\left(C^{0}([0,1]),\|\cdot\|_{1}\right) \) ?
ii) ... als Funktion \( \Phi:\left(C^{0}([0,1]),\|\cdot\|_{\infty}\right) \rightarrow\left(C^{0}([0,1]),\|\cdot\|_{1}\right) \) ?
iii) \( \ldots \) als Funktion \( \Phi:\left(C^{0}([0,1]),\|\cdot\|_{1}\right) \rightarrow\left(C^{0}([0,1]),\|\cdot\|_{\infty}\right) \) ?
iv).. als Funktion \( \Phi:\left(C^{0}([0,1]),\|\cdot\|_{\infty}\right) \rightarrow\left(C^{0}([0,1]),\|\cdot\|_{\infty}\right) \) ?

Bin hier bisschen planlos was die gegebene Funktion „aussagt“ und wie ich die Funktionen auf Stetigkeit überprüfen kann.

Könnte mir jemand helfen?

Comments

Was ist denn bei euch die 1-Norm?

Ist es \(\|f\|_1=\int_0^1 |f(x)|dx\) ?

---

Ja und die ∞-Norm ist die normale Supremumsnorm

Answer 1

Die identische Abbildung \(\Phi:\; (X,d)\to (X,d')\) ist genau dann stetig,

wenn die \(d'\)-offenen Mengen auch \(d\)-offen sind,

wobei \(X=C^0([0,1])\) ist und die \(d, d'\) die jeweils von den Normen

kommenden Metriken.

Comments

Wären dann i) und iv) nicht automatisch stetig, weil die Normen jeweils die gleichen sind und deswegen die gleichen offenen Mengen haben?

---

Ja. Das ist in der Tat so.

---

Das habe ich gefunden:

https://de.wikipedia.org/wiki/%C3%84quivalente_Normen

Hier der Abschnitt "Unendlichdimensional"

Die Supremumsnorm ist stärker als die L1-Norm.

---

Also wäre ii) stetig, iii) aber nicht? Hätte das so begründet, dass durch die Abschätzung jede offene Menge in der ∞-Norm auch in der 1-Norm enthalten sein muss, aber nicht umgekehrt. Ist das so richtig oder habe ich hier einen Denkfehler gemacht?

---

Ich sehe das ganz genau so ;-)