Funktionenschar: Untersuche, ob y=12x-3 Tangente an Graph von g16(x) = x4 - 8·x3 + 16·x2 ist

Question

$g_{a}(x)=x^{4}-8 x^{3}+a x^{2}$

Untersuchen Sie, ob die Gerade $y=12 x-3$ Tangente an den Graphen von $f_{16}(x)$ ist!

Answer 1

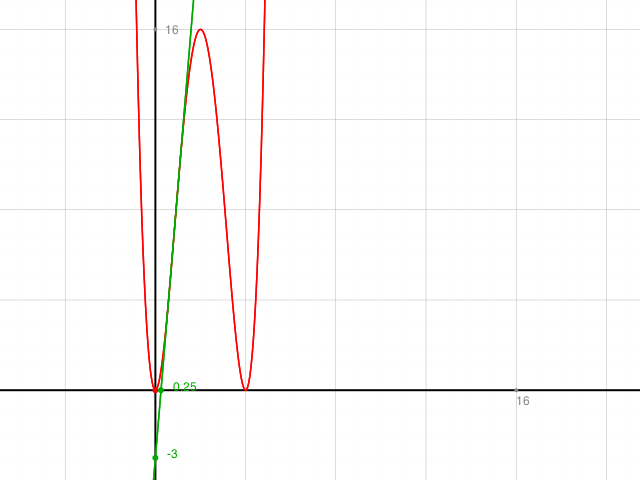
g16(x) = x⁴ - 8·x³ + 16·x²
g16'(x) = 4·x³ - 24·x² + 32·x

Angebliche Tangente

y = 12x- 3

y' = 12

Steigungen gleichsetzen und nach x auflösen

4·x³ - 24·x² + 32·x = 12

x³ - 6·x² + 8·x = 3

x³ - 6·x² + 8·x -3 = 0     |Nullstelle raten  x1 = 1

Polynomdivision

(x³ - 6·x² + 8·x - 3): (x-1) = x² -5x + 3

pq-Formel

x2 = 1/2 (5-sqrt(13))

x3 = 1/2 (5+sqrt(13))

Nun die 3 gefundenen Stellen in der Gleichungen der Kurve und der angeblichen Tangente einsetzen.

g16(x) = x⁴ - 8·x³ + 16·x²

g16(1) = 1⁴ - 8·1³ + 16·1² = 9

t: y = 12x -3, 12*1-3 =9

qed. Gerade ist Tangente und berührt die Kurve im Punkt (1|9)

Man muss daher die andern beiden Stellen gar nicht mehr prüfen.

Kontrolle: Graph.