Steckbriefaufgabe: Ganzrationale Funktion 4ten Grades

Question

Gesucht ist eine ganzrationale Funktion 4.Grades. Die Funktion ist symmetrisch zur y-Achse. Sie hat eine Nullstelle im Punkt x=4 und schneidet die y-Achse im Punkt Y (0/2). Zudem ist ein Maximum bei x=2 bekannt. Bestimmen Sie die Funktion.

Ich hab bis jetzt:

Ansatz:
f (x) = ax4+bx2+c
f '(x) = 4ax3+2bx
f ''(x) = 12ax2+2b

N (4/0) →  f (4) = 0
                  256a + 16b = 0
Y (0/2) → f (0) = 2
                 c = 2
H (2/?) → f (2) = ?
     
Waagrechte Tangente bei x=2 → f '(2) = 0
                                                            512a + 4b = 0

Answer 1

Außer, dass du an einer Stelle das c vergessen hast und dich bei 2^3*4 etwas verrechnet hast, ist das soweit richtig. Du hast drei Gleichungen für drei Variablen:

(I) 256a+16b+c=0

(II) c=2

(III) 32a+4b = 0

 

Rechnet man jetzt (I)-8*(III), so folgt:
256a+16b+c-8*32a-8*4b = 0

256a+16b+c-256a-32b = 0

c = 16b

b = 1/8

Und mit (I) oder (III) kann man jetzt auch a berechnen. Es gilt:

a = -4*b/32 = -1/64

Lässt man sich diese Funktion zeichnen, so erkennt man, dass

f(x) = -x⁴/64+x²/8 + 2

tatsächlich die gewünschten Eigenschaften hat.

 

Comments

Danke. Aber woher weiß ich, dass ich da "-8" rechnen muss?

---

Ich habe das natürlich so gewählt, dass das a aus der Gleichung völlig rausfällt.

Man kann das System natürlich auch z.B. nach dem Gleichsetzungsverfahren lösen, also beide Gleichungen z.B. nach a umstellen und dann gleichsetzen.

Wichtig ist nur, dass man eine Variable aus den beiden Gleichungen eliminiert.

Answer 2

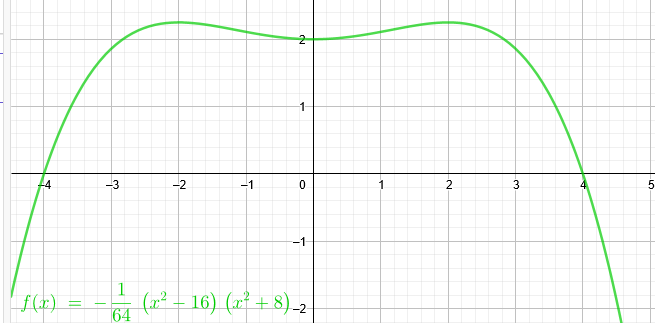
"Gesucht ist eine ganzrationale Funktion 4.Grades. Die Funktion ist symmetrisch zur y-Achse. Sie hat eine Nullstelle im Punkt x=4 und schneidet die y-Achse im Punkt Y (0|2). Zudem ist ein Maximum bei x=2 bekannt. Bestimmen Sie die Funktion."

Sie hat eine Nullstelle im Punkt x=4 →

Wegen Symmetrie ist bei x=-4 auch eine Nullstelle.

Weg über die Nullstellenform der Parabel 4. Grades:

\(f(x)=a*(x-4)*(x+4)*(x-N)*(x+N)\)

\(f(x)=a*(x^2-16)*(x^2- N^{2} )\)

\(Y(0|2)\)

\(f(0)=a*(0-16)*(0- N^{2} )=16*a* N^{2}\)

\(16*a* N^{2}=2→8*a* N^{2}=1→a=\frac{1}{8*N^{2}}\)

\(f(x)=\frac{1}{8*N^{2}}*[(x^2-16)*(x^2- N^{2} )]\)

\(f´(x)=\frac{1}{8*N^{2}}*[2x*(x^2- N^{2} )+(x^2-16)*2x]\)

\(f´(2)=\frac{1}{8*N^{2}}*[2*2*(2^2- N^{2} )+(2^2-16)*2*2]\)

\(\frac{1}{8*N^{2}}*[-32- 4*N^{2} ]=0\)

\(N^2=-8 \)

\(a=\frac{1}{8*(-8)}=-\frac{1}{64}\)

\(f(x)=-\frac{1}{64}*(x^2-16)*(x^2+8)\)