Question

Wie kommt man auf diesen Bruch?

Ich verstehe vor allem nicht, wie es zu den 2¹/2 kommt.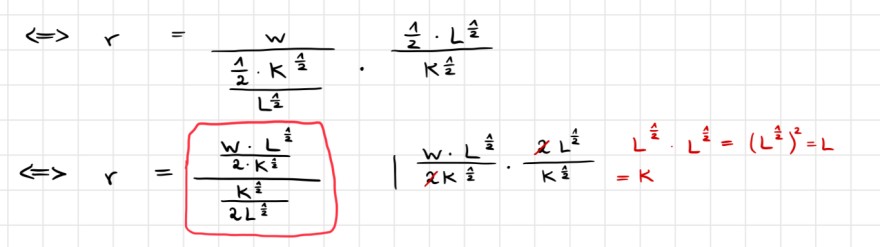

Text erkannt:

$\begin{array}{l}\Leftrightarrow r=\frac{w}{\frac{\frac{1}{2} \cdot K^{\frac{1}{2}}}{L^{\frac{1}{2}}}} \cdot \frac{\frac{1}{2} \cdot L^{\frac{1}{2}}}{K^{\frac{1}{2}}} \\ \Leftrightarrow r=\frac{\frac{W \cdot L^{\frac{1}{2}}}{2 \cdot K^{\frac{1}{2}}}}{\frac{K^{\frac{1}{2}}}{2 L^{\frac{1}{2}}}} \mid \frac{w \cdot L^{\frac{1}{2}}}{x K^{\frac{1}{2}}} \cdot \frac{x L^{\frac{1}{2}}}{K^{\frac{1}{2}}}=K L^{\frac{1}{2}} \cdot L^{\frac{\hat{1}}{2}}=\left(L^{\frac{1}{2}}\right)^{2}=L\end{array}$

Answer 1

1/2 kannst du sofort wegkürzen

Doppelbruchgesetz anwenden:

a/(b/c) = (ac)/b

a^(1/2)*a^(1/2) = a^(1/2+1/2) = a¹ = a

oder:

a^(1/2)*a^(1/2) = (a^(1/2))² = a¹ = a

Wo steht 2¹/2 ?

Answer 2

Es wurden die Regeln

        $a\cdot \frac{b}{c} = \frac{a\cdot b}{c}$

und

    $\frac{a}{c}\cdot \frac{b}{d} = \frac{a\cdot b}{c\cdot d}$

verwendet.

        $\begin{aligned} & \frac{W}{\frac{\frac{1}{2}K^{\frac{1}{2}}}{L^{\frac{1}{2}}}}\cdot\frac{\frac{1}{2}L^{\frac{1}{2}}}{K^{\frac{1}{2}}}\\ = & \frac{W}{\frac{\frac{1}{2}K^{\frac{1}{2}}}{L^{\frac{1}{2}}}}\cdot\left(\frac{1}{2}\cdot\frac{L^{\frac{1}{2}}}{K^{\frac{1}{2}}}\right)\\ = & \frac{W}{\frac{\frac{1}{2}K^{\frac{1}{2}}}{L^{\frac{1}{2}}}}\cdot\frac{L^{\frac{1}{2}}}{2\cdot K^{\frac{1}{2}}}\\ = & \frac{W}{\frac{1}{2}\cdot\frac{K^{\frac{1}{2}}}{L^{\frac{1}{2}}}}\cdot\frac{L^{\frac{1}{2}}}{2\cdot K^{\frac{1}{2}}}\\ = & \frac{W}{\frac{K^{\frac{1}{2}}}{2L^{\frac{1}{2}}}}\cdot\frac{L^{\frac{1}{2}}}{2\cdot K^{\frac{1}{2}}}\\ = & \frac{W\cdot\frac{L^{\frac{1}{2}}}{2\cdot K^{\frac{1}{2}}}}{\frac{K^{\frac{1}{2}}}{2L^{\frac{1}{2}}}}\\ = & \frac{\frac{W\cdot L^{\frac{1}{2}}}{2\cdot K^{\frac{1}{2}}}}{\frac{K^{\frac{1}{2}}}{2L^{\frac{1}{2}}}} \end{aligned}$