Sind die komplexen Zahlen Element von Menge M?

Question

Aufgabe:

Hallo, man muss bestimmen, ob z1 und z2 Mengen von M1 und M2 sind.

z1 = 2 + i

z2 =1/2+ i 1/2

M1 = {z ∈ C | Im(z) ≥ Re(z)}

M2 = {z ∈ C | |z| ≥ 1}

Problem/Ansatz:

Ich habs so raus, dass Z2 und z1 Mengen von M1 sind und z1 von M2 und z2 nicht von m2???

Comments

Was für Mengen drücken die Buchstaben aus?

---

Ich schlage vor, Du liest Dir Deine Frage noch einmal durch und vervollständigt sie.

---

Wenn das eine Zusatzfrage zu deiner ersten Frage ist, dann stell die Bitte auch dort.

https://www.mathelounge.de/1028909/komplexe-zahlen-in-zahlenebene-sk…

Answer 1

Wenn Du Dich auf die vorige Frage beziehst (die Informationen gehören hier aber auch nochmal hin):

Beachte, $z_1, z_2$ sind Zahlen, keine Mengen. Die Frage ist also, ob $z_i\in M_j$ gilt ("Element von...").

Für $M_1$: Ermittle Real- und Imaginärteil von $z_1,z_2$ (direkt ablesen). Ergebnis zur Kontrolle: $z_1 \notin M_1, z_2\in M_1$.

Für $M_2$: Ermittle den Betrag von $z_1,z_2$ (das ist $\sqrt{Re^2+Im^2}$). Ergebnis: $z_1\in M_2, z_2\notin M_2$.

Comments

Wo ist beim 1. Bild (z1 und m1) der Fehler?

Und ist das andere so richtig ?

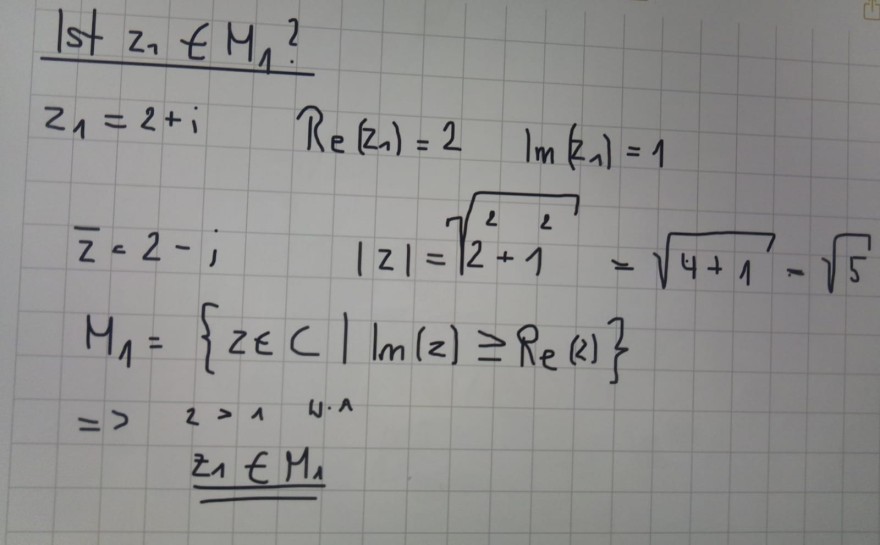
Text erkannt:

$\begin{array}{l}\text { Ist } z_{1} \in M_{1} \text { ? } \\ z_{1}=2+i \quad \operatorname{Re}\left(z_{1}\right)=2 \quad \operatorname{lm}\left(z_{1}\right)=1 \\ \bar{z}=2-i \quad|z|=\sqrt{2^{2}+1^{2}}=\sqrt{4+1}-\sqrt{5} \\ M_{1}=\{z \in C \mid \ln (z) \geq \operatorname{Re}(z)\} \\ \Rightarrow \quad 2>1 \text { W.A } \\ \underline{\underline{z_{1}} \in M_{1}} \\\end{array}$

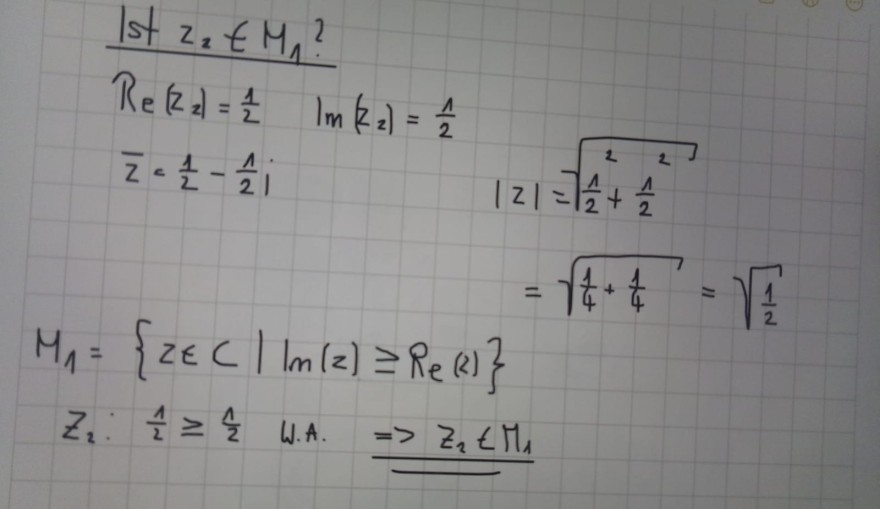
Text erkannt:

$\begin{array}{l}\text { Ist } z_{2} \in M_{1} \text { ? } \\ \operatorname{Re}\left(z_{z}\right)=\frac{1}{2} \quad \operatorname{lm}\left(R_{z}\right)=\frac{1}{2} \\ \bar{z}=\frac{1}{2}-\frac{1}{2} i \\ |z|=\sqrt{\frac{\Lambda^{2}}{2}+\frac{1^{2}}{2}} \\ =\sqrt{\frac{1}{4}+\frac{1}{4}}=\sqrt{\frac{1}{2}} \\ M_{1}=\{z \in C \mid \ln (z) \geq \operatorname{Re}(z)\} \\ Z_{2}: \frac{1}{2} \geq \frac{1}{2} \text { W.A. } \quad \Rightarrow Z_{2} \in \Pi_{1} \\\end{array}$

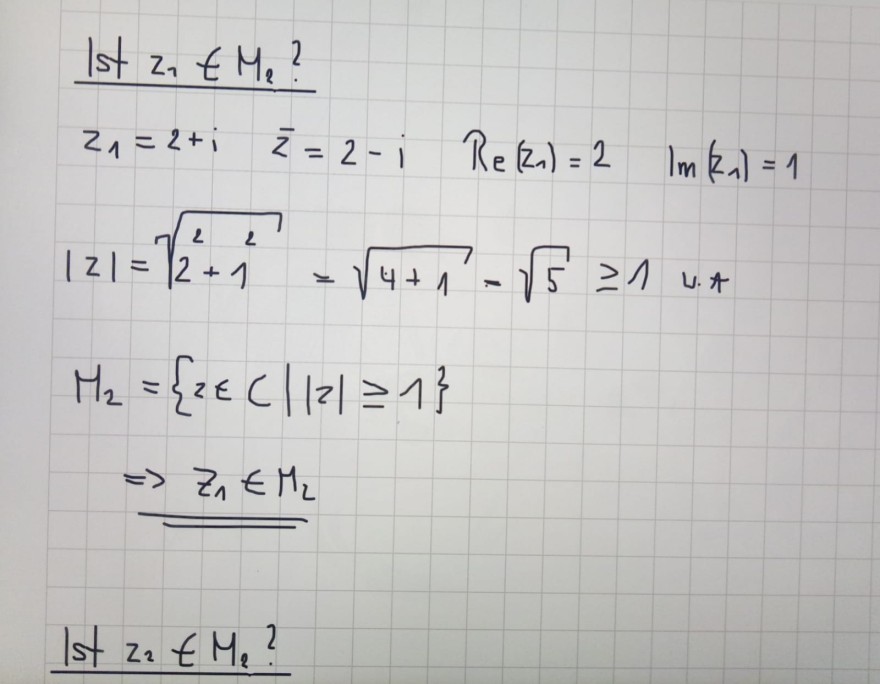
Text erkannt:

Ist $z_{1} \in M_{2}$ ?
$\begin{aligned} z_{1} & =2+i \quad \bar{z}=2-i \quad \operatorname{Re}\left(z_{1}\right)=2 \quad \operatorname{lm}\left(z_{1}\right)=1 \\ |z| & =\sqrt{2^{2}+1}=\sqrt{4+1}-\sqrt{5} \geq 1 \quad \text { u.A } \\ M_{2} & =\{z \in C|| z \mid \geq 1\} \\ & \Rightarrow z_{1} \in M_{2} \end{aligned}$
Ist $z_{2} \in M_{2}$ ?

Text erkannt:

Ist $z_{2} \in M_{2}$ ?
$\begin{array}{l} M_{2}=\{z \in C|| z \mid \geq 1\} \\ z_{2}=\frac{1}{2}+i \frac{1}{2} \\ \operatorname{Re}\left(z_{z}\left|=\frac{1}{2} \quad \operatorname{lm}\right| z_{z}\right)=\frac{1}{2} \\ \bar{z}=\frac{1}{2}-\frac{1}{2} i \quad \quad|z|=\sqrt{\frac{1}{2}+\frac{1}{2}} \\ =\sqrt{\frac{1}{4}+\frac{1}{4}}=\sqrt{\frac{1}{2}} \\ H_{2}=\{z \in C|| z \mid \geq 1\} \end{array}$
$z_{2}: \frac{1}{2} \geq 1$ f.A. $\Rightarrow z_{2} \notin M_{2}$

---

Naja, 1 ist eben nicht größer gleich 2, daher ist $z_1\notin M_1$.

Sonst ist alles richtig.

---

ok, danke

aber da steht doch 2 ist größer als 1

---

Nein, da steht $Im \ge Re$, also hier $1\ge 2$.